2015-02-27
351
1.1 Постановка задачи
Пусть дана некоторая функция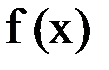 
и требуется найти все или некоторые значения 
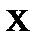, для которых 
.
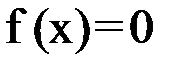Значение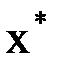 
, при котором 
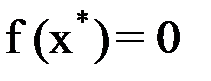, называется корнем (или решением) уравнения. Относительно функции 
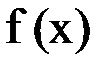часто предполагается, что 
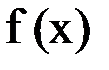дважды непрерывно дифференцируема в окрестности корня.
Корень 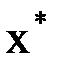уравнения называется простым, если первая производная функции 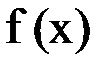в точке 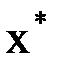не равна нулю, т. е. 
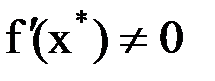. Если же 
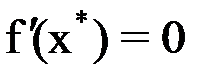, то корень 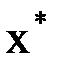называется кратным корнем.
Геометрически корень уравнения есть точка пересечения графика функции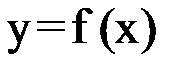 
с осью абсцисс. На рисунке 1.1 изображен график функции 
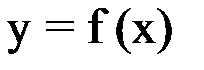, имеющей четыре корня: два простых 
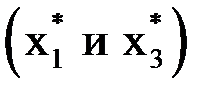и два кратных 
.
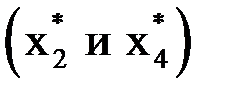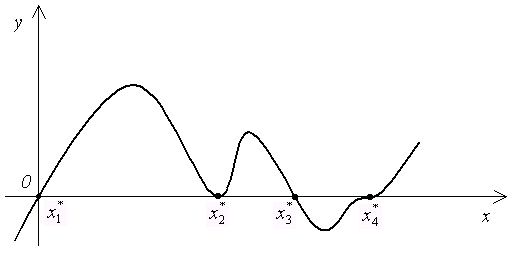
Рисунок 1.1 - График функции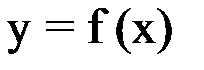
Большинство методов решения уравнения ориентировано на отыскание простых корней.
