Пусть уравнение 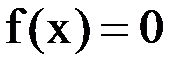 можно заменить эквивалентным ему уравнением
можно заменить эквивалентным ему уравнением
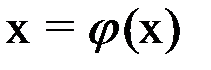 . (1.2)
. (1.2)
Выберем каким-либо образом начальное приближение 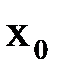 . Вычислим значение функции
. Вычислим значение функции 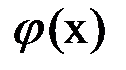 при
при 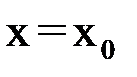 и найдем уточненное значение
и найдем уточненное значение 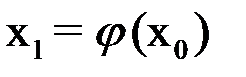 . Подставим теперь
. Подставим теперь 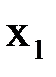 в уравнение (1.1) и получим новое приближение
в уравнение (1.1) и получим новое приближение 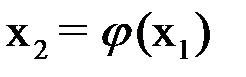 и т. д. Продолжая этот процесс неограниченно, получим последовательность приближений к корню:
и т. д. Продолжая этот процесс неограниченно, получим последовательность приближений к корню:
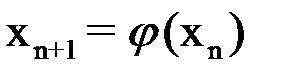 . (1.3)
. (1.3)
Формула (1.3) является расчетной формулой метода простой итерации.
Если последовательность 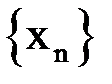 сходится при
сходится при 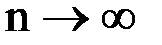 , т. е. существует
, т. е. существует
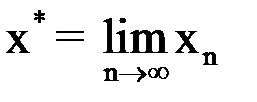 (1.4)
(1.4)
и функция 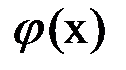 непрерывна, то, переходя к пределу в (1.3) и учитывая (4), получим:
непрерывна, то, переходя к пределу в (1.3) и учитывая (4), получим: 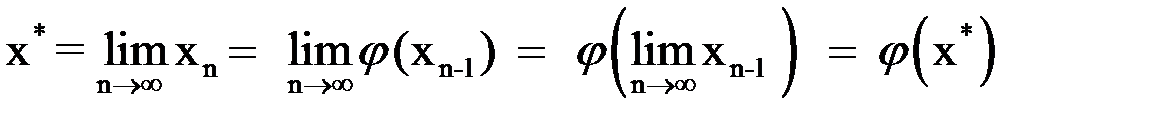 .
.
Таким образом, 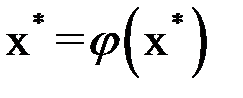 , следовательно,
, следовательно, 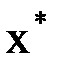 – корень уравнения (1.2).
– корень уравнения (1.2).
Сходимость метода. Сходимость метода простой итерации устанавливает следующая теорема.
Теорема. Пусть функция 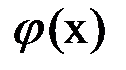 определена и дифференцируема на отрезке
определена и дифференцируема на отрезке 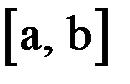 , причем все ее значения
, причем все ее значения 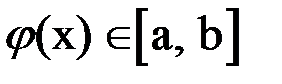 . Тогда, если выполняется условие
. Тогда, если выполняется условие 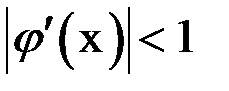 при
при 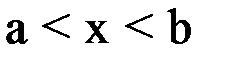 :
:
1) процесс итерации 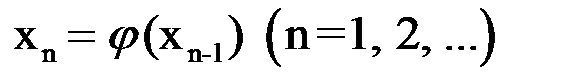 сходится независимо от начального значения
сходится независимо от начального значения 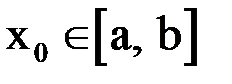 ;
;
2) предельное значение 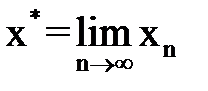 является единственным корнем уравнения
является единственным корнем уравнения 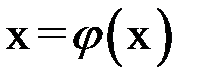 на отрезке
на отрезке 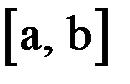 .
.
Доказательство. Так как 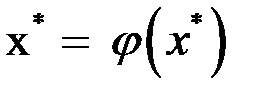 и
и 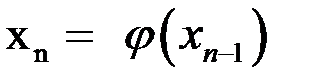 , то можно записать
, то можно записать
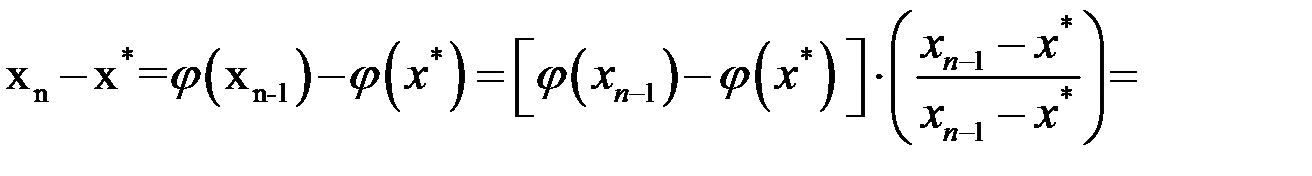
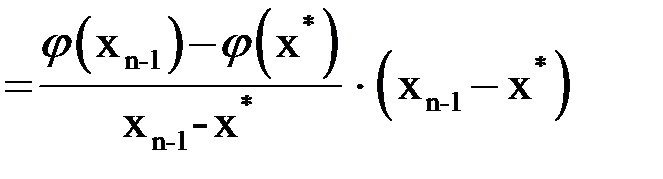 .
.
По теореме о среднем (она утверждает, что если производная функции 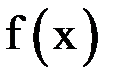 непрерывна на некотором интервале
непрерывна на некотором интервале 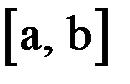 , то тангенс угла наклона хорды, проведенной между точками
, то тангенс угла наклона хорды, проведенной между точками 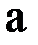 и
и 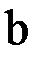 , (т.е.
, (т.е. 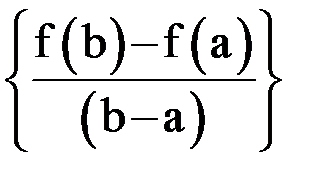 равен производной функции в некоторой промежуточной точке, лежащей между
равен производной функции в некоторой промежуточной точке, лежащей между 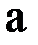 и
и 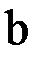 ) частное в последнем выражении будет равно
) частное в последнем выражении будет равно 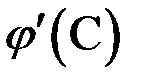 , где
, где  – некоторая промежуточная точка в интервале поиска корня. Следовательно,
– некоторая промежуточная точка в интервале поиска корня. Следовательно, 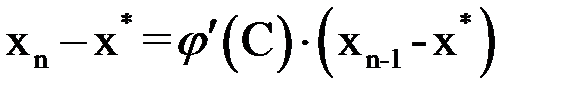 .
.
Если ввести обозначение 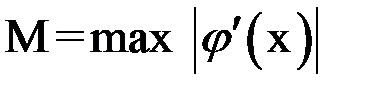 для всего интервала поиска, то предыдущее равенство может быть переписано в виде:
для всего интервала поиска, то предыдущее равенство может быть переписано в виде: 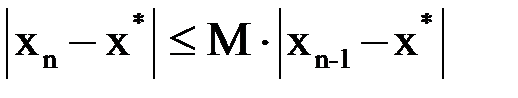
Аналогично 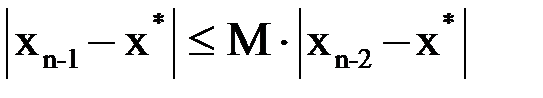 . Тогда для
. Тогда для 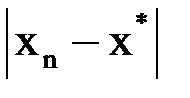 будет справедливо неравенство:
будет справедливо неравенство: 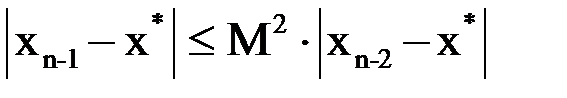 и т. д. Продолжая эти выкладки дальше, в результате получаем
и т. д. Продолжая эти выкладки дальше, в результате получаем 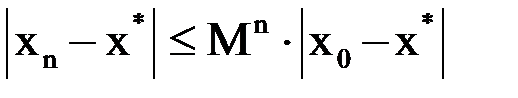 , где
, где 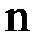 – натуральное число. Таким образом, чтобы метод сходился, необходимо выполнение неравенства:
– натуральное число. Таким образом, чтобы метод сходился, необходимо выполнение неравенства: 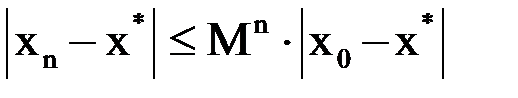 .
.
Отсюда следует, что 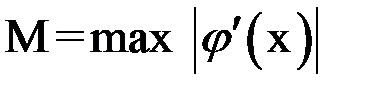 должно быть меньше единицы. В свою очередь, для всех остальных значений
должно быть меньше единицы. В свою очередь, для всех остальных значений 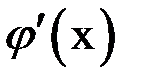 меньших
меньших 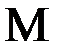 , можно записать:
, можно записать: 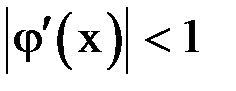 . Число
. Число 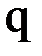 определим из соотношения
определим из соотношения 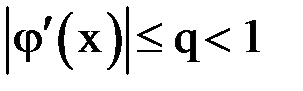 . Тогда справедливо неравенство (вывод см. ниже):
. Тогда справедливо неравенство (вывод см. ниже): 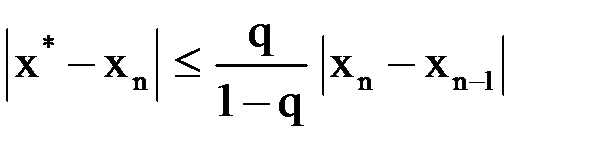 . Если поставить условие, что истинное значение корня
. Если поставить условие, что истинное значение корня 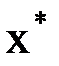 должно отличаться от приближенного значения на величину
должно отличаться от приближенного значения на величину 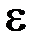 , т.е.
, т.е. 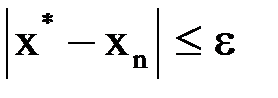 , то приближения
, то приближения 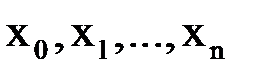 надо вычислять до тех пор, пока не будет выполнено неравенство
надо вычислять до тех пор, пока не будет выполнено неравенство
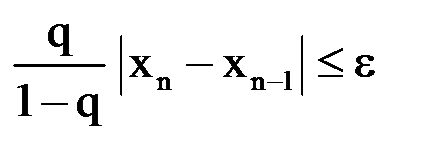 или
или 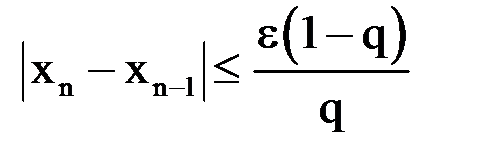 и тогда
и тогда 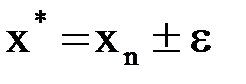 .
.
Вывод неравенства.Рассмотрим два последовательных приближения: 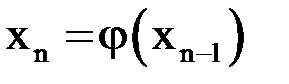 и
и 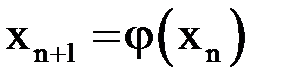 . Отсюда
. Отсюда 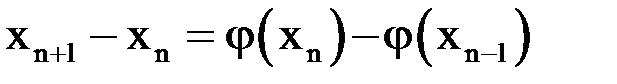 .
.
Используя теорему о среднем, получим:
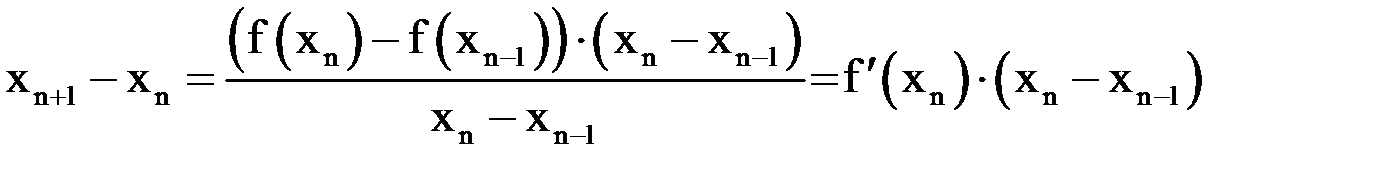 ,
,
тогда на основании условия 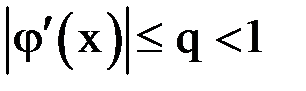 можно записать:
можно записать:
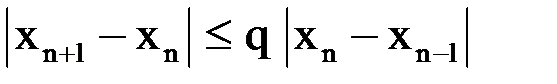 .
.
С другой стороны, пусть 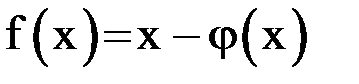 . Очевидно, что
. Очевидно, что 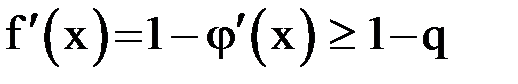 . Отсюда, учитывая, что
. Отсюда, учитывая, что 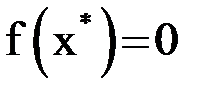 , получим
, получим
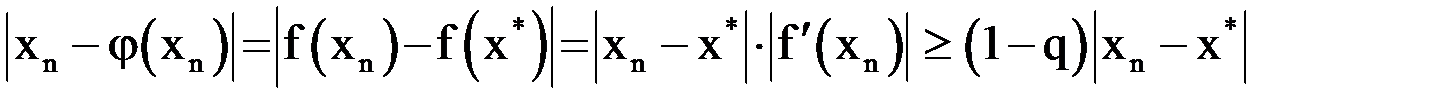 ,
,
где 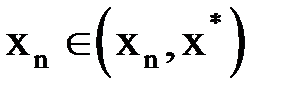 .
.
Тогда 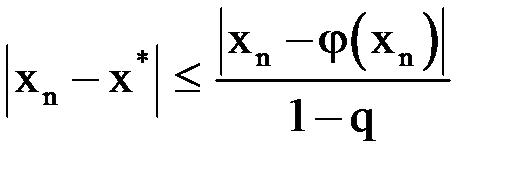 или
или 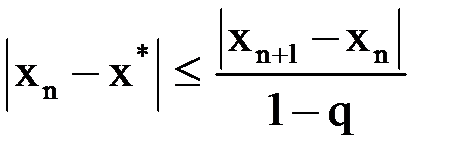 .
.
Используя предыдущую формулу, можно получить:
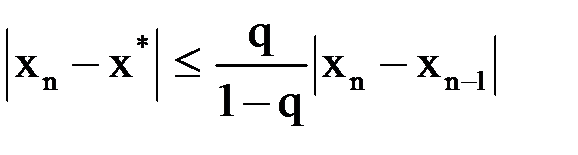 . (1.5)
. (1.5)
Перейдём к пределу в равенстве (1.3), в силу непрерывности функции 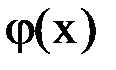 получим
получим 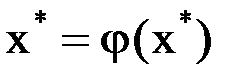 , то есть
, то есть 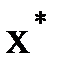 – корень уравнения (1.2). Других корней на
– корень уравнения (1.2). Других корней на 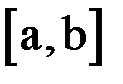 нет, так как если
нет, так как если 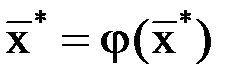 , то
, то 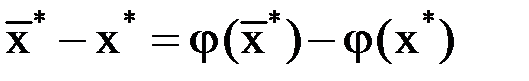 , тогда
, тогда 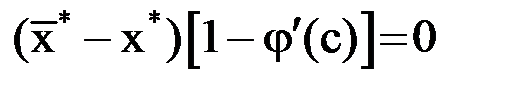 , где
, где 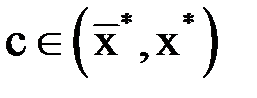 . Равенство нулю будет достигнуто, если
. Равенство нулю будет достигнуто, если 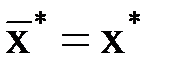 . То есть
. То есть 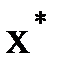 – корень единственный.
– корень единственный.
Приведение уравнения 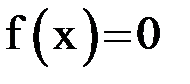 к виду
к виду 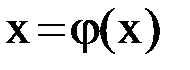 для обеспечения выполнения неравенства
для обеспечения выполнения неравенства 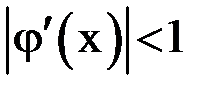 .
.
В общем случае получить подходящую итерационную форму возможно, проведя равносильное преобразование исходного уравнения, например, умножив его на коэффициент 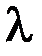 :
: 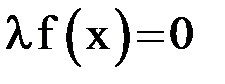 . Прибавив затем к обеим частям уравнения
. Прибавив затем к обеим частям уравнения 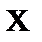 и обозначив
и обозначив 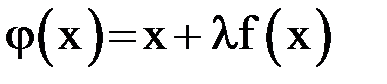 можно потребовать выполнения достаточного условия
можно потребовать выполнения достаточного условия 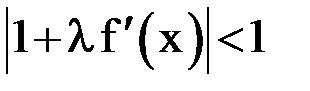 . Отсюда определяется необходимое значение
. Отсюда определяется необходимое значение 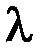
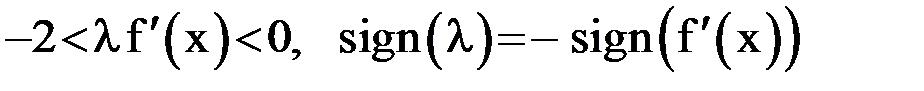 . Так как условие
. Так как условие 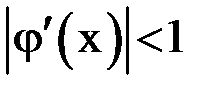 должно выполняться на всем отрезке
должно выполняться на всем отрезке 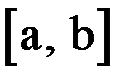 , то для выбора
, то для выбора 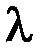 следует использовать наибольшее значение
следует использовать наибольшее значение 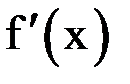 на этом отрезке, т.е.
на этом отрезке, т.е.
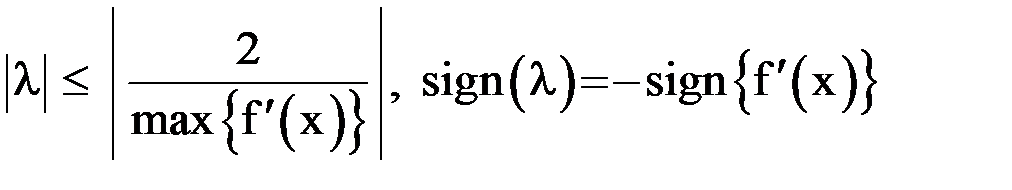 . Это соотношение определяет диапазон значений коэффициента
. Это соотношение определяет диапазон значений коэффициента 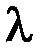 , изменяющий величину
, изменяющий величину 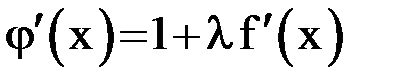 в пределах
в пределах 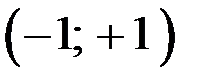 .
.
Обычно принимают 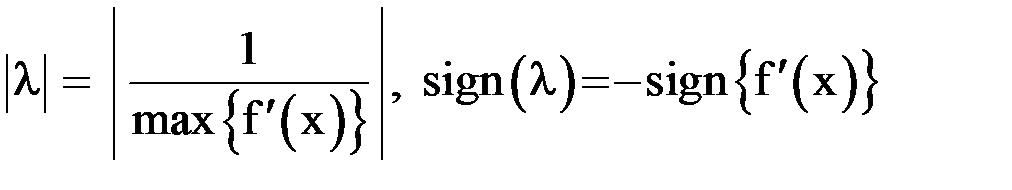 .
.
На рисунках 1.3, 1.4, 1.5, 1.6 показаны четыре случая взаимного расположения линий 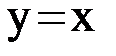 и
и 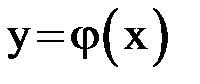 и соответствующие итерационные процессы. Рисунки 1.3 и 1.4 соответствуют случаю
и соответствующие итерационные процессы. Рисунки 1.3 и 1.4 соответствуют случаю 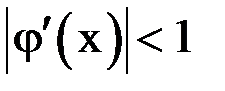 , и итерационный процесс сходится. При этом, если
, и итерационный процесс сходится. При этом, если 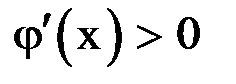 (рис. 1.3), сходимость носит односторонний характер, а если
(рис. 1.3), сходимость носит односторонний характер, а если 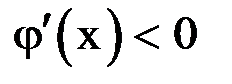 (рис. 1.4), сходимость носит двусторонний, колебательный характер. Рисунки 5 и 6 соответствуют случаю
(рис. 1.4), сходимость носит двусторонний, колебательный характер. Рисунки 5 и 6 соответствуют случаю 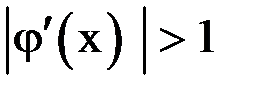 – итерационный процесс расходится. При этом может быть односторонняя (рис. 1.5) и двусторонняя (рис. 1.6) расходимость.
– итерационный процесс расходится. При этом может быть односторонняя (рис. 1.5) и двусторонняя (рис. 1.6) расходимость.
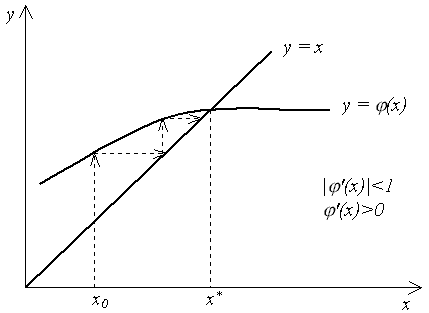
Рисунок 1.3 - Взаимное расположения линий 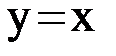 и
и 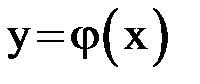 и итерационныи процесс соответствущий случаю
и итерационныи процесс соответствущий случаю 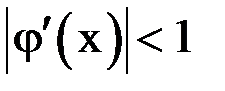 , с сходимостью одностороннего характера
, с сходимостью одностороннего характера
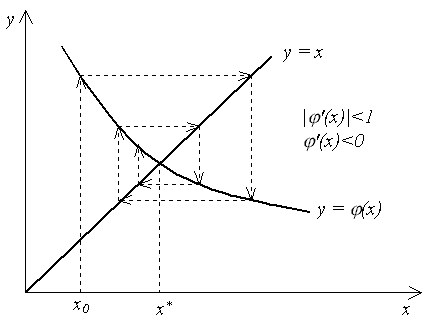
Рисунок 1.4 - Взаимное расположения линий 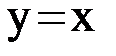 и
и 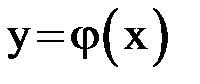 и итерационныи процесс соответствущий случаю
и итерационныи процесс соответствущий случаю 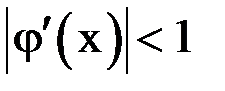 , с сходимостью двустороннего характера
, с сходимостью двустороннего характера
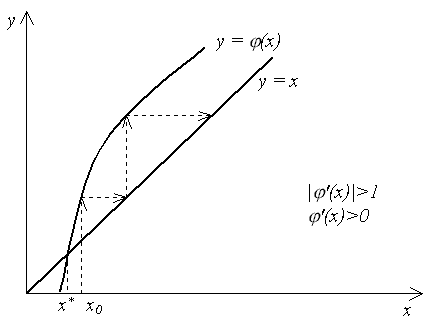
Рисунок 1.5 - Взаимное расположения линий 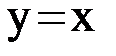 и
и 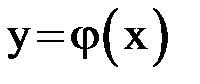 и итерационныи процесс соответствущий случаю
и итерационныи процесс соответствущий случаю 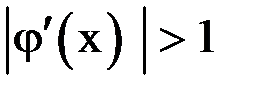 , с расходимостью одностороннего характера
, с расходимостью одностороннего характера
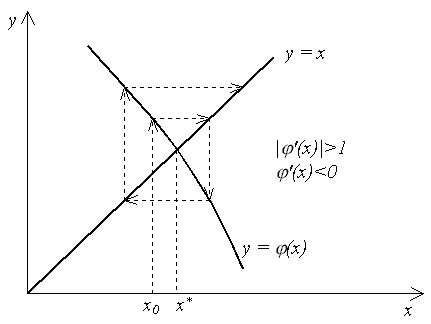
Рисунок1.6 - Взаимное расположения линий 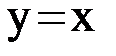 и
и 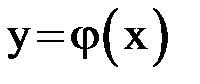 и итерационныи процесс соответствущий случаю
и итерационныи процесс соответствущий случаю 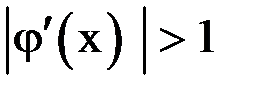 , с сходимостью двустороннего характера
, с сходимостью двустороннего характера
Погрешность метода. Оценка погрешности была доказана (1.5).
Критерий окончания. Из оценки (1.5) следует, что вычисления надо продолжать до выполнения неравенство 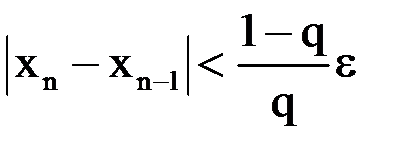 . Если же
. Если же 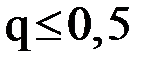 , то оценка упрощается:
, то оценка упрощается: 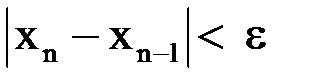 .
.
Пример 1.1. Используем метод простой итерации для решения уравнения 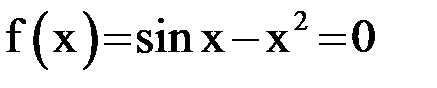 с точностью
с точностью 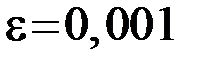 . Преобразуем уравнение к виду:
. Преобразуем уравнение к виду:
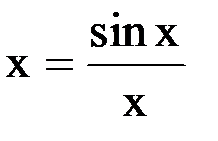 , т. е.
, т. е. 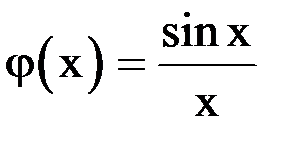 .
.
Нетрудно убедиться, что корень уравнения находится на отрезке 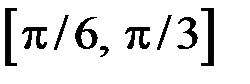 . Вычислив значения
. Вычислив значения 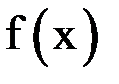 на концах отрезка, получим:
на концах отрезка, получим: 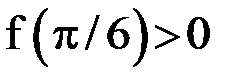 , а
, а 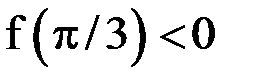 , т. е. функция на концах отрезка имеет разные знаки, поэтому внутри отрезка есть корень. Расположение корня наглядно иллюстрирует рисунок 1.7.
, т. е. функция на концах отрезка имеет разные знаки, поэтому внутри отрезка есть корень. Расположение корня наглядно иллюстрирует рисунок 1.7.
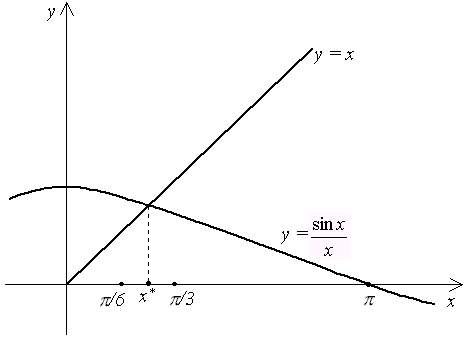
Рисунок 1.7 - Расположение корня
Подсчитаем первую и вторую производные функции 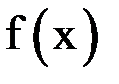 :
:
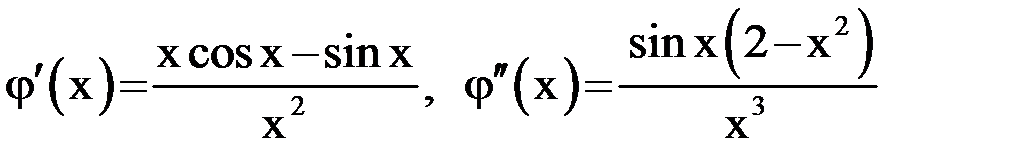 .
.
Так как 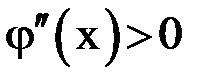 на отрезке
на отрезке 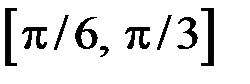 , то производная
, то производная 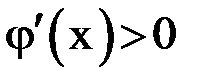 монотонно возрастает на этом отрезке и принимает максимальное значение на правом конце отрезка, т. е. в точке
монотонно возрастает на этом отрезке и принимает максимальное значение на правом конце отрезка, т. е. в точке 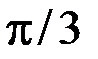 . Поэтому справедлива оценка:
. Поэтому справедлива оценка:
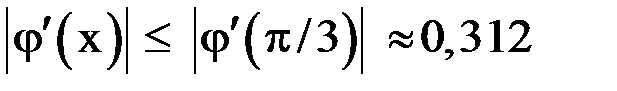 .
.
Таким образом, условие выполнено, 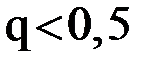 и можно воспользоваться критерием окончания вычислений. В таблице 2 приведены приближения, полученные по расчетной формуле. В качестве начального приближения выбрано значение
и можно воспользоваться критерием окончания вычислений. В таблице 2 приведены приближения, полученные по расчетной формуле. В качестве начального приближения выбрано значение 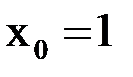 .
.
Таблица 1.2 – Приближения корня
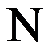 | ||||||
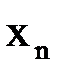 | 0,8415 | 0,8861 | 0,8712 | 0,8774 | 0,8765 |
Критерий окончания выполняется при 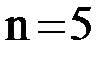 ,
, 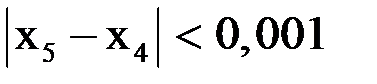 . Сходимость двусторонняя, качественный характер такой сходимости представлен на рис. 4. Приближенное значение корня с требуемой точностью
. Сходимость двусторонняя, качественный характер такой сходимости представлен на рис. 4. Приближенное значение корня с требуемой точностью 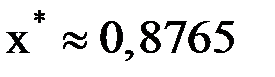 .
.
Пример 1.2. Решить методом простой итерации уравнение 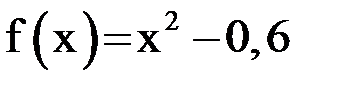 на отрезке
на отрезке 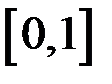 с точностью 0,025. Для решения исходное уравнение приводится к виду
с точностью 0,025. Для решения исходное уравнение приводится к виду 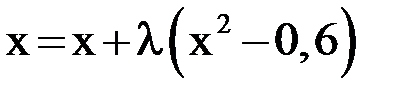 . Для выбора величины
. Для выбора величины 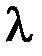 используем приведенную выше формулу
используем приведенную выше формулу 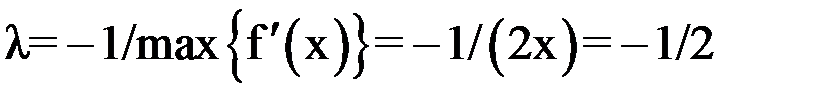 . Тогда расчетная формула имеет вид
. Тогда расчетная формула имеет вид 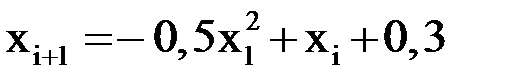 . В качестве начального приближения можно выбрать верхнюю границу заданного отрезка
. В качестве начального приближения можно выбрать верхнюю границу заданного отрезка 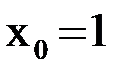 .
.
 | |||
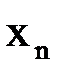 | 0,8 | 0,78 |
Так как 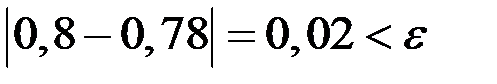 , то
, то 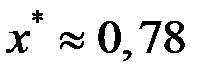 .
.
 2015-02-27
2015-02-27 3044
3044
