Высказывания

Под высказыванием понимают повествовательное предложение, о котором имеет смысл говорить, истинно оно или ложно.

Как видим, этому понятию не дается строго математического опре­деления, а дается лишь способ отличать высказывания от «невысказыва­ний». Таким образом, единственное свойство высказывания ― быть истин­ным или ложным.

Обычно высказывания обозначают большими латинскими буквами: А, В, С и т.д. Если высказывание А ― истинно, то это символически обозначают так: [А] = 1 или [А] = и, если А ― ложно, то [А] = 0 или [А] = л.

Рассмотрим ряд предложений:

1. х<5;

2. Если (х<у) и (у<z), то (х<z), где х, у, z ∈ R;

3. Для любого х 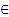R найдется y 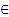R, такой, что х+у=0;

4. Да здравствует 1 Мая!

5. Который час?

6. Треугольник называется равносторонним, если все его стороны равны между собой;

7. В равностороннем треугольнике любая его медиана является бис­сектрисой и высотой.

В этом списке предложения 2, 3, 7 ― истинные высказывания. Предложение 1 станет высказыванием (истинным или ложным), если вместо x подставить конкретное действительное число. Например, [2<5] = 1, [7<5] = 0. Все вопросительные, восклицательные предложения и определения не являются высказываниями. Поэтому предложения 4, 5, 6 ― не высказывания.

В естественном языке (русский, немецкий, английский и т.д.) все предложения можно поделить на простые и сложные. Сложные предложения состоят из нескольких простых, соединенных между собой при помощи союзов или связок (или, и, если... то, не и т.д.)

Аналогичным образом и в математической логике, ― образование сложного выска­зывания из простых (элементарных) происходит при помощи логических операций: конъюнкции, дизъюнкции, импликации, эквиваленции, отрицания, которые соответствуют союзам, связкам естественного языка, но в строго определенном смысле.

Так как каждое элементарное высказывание А может иметь только два истинностных значения (1 или 0), то для каждой пары высказываний А, В будет 4 комбинации истинностных значений. Указав для каждой такой комбинации соответствующее истинностное значение их конъюнкции, дизъюнкции, импликации, эквиваленции, отрицания, мы получим таблицу, определяющую эти логические операции:

[A]	[B]	[A&B]	[A∨B]	[A→B]	[A↔B]	[ ]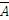

Конъюнкция (логическое произведение) обозначается А&В и читается: «А и В», дизъюнкция (логическая сумма), обозначается A∨B, читается: «А или В»; импликация ― А→В, читается «если А, то В», «из А следует В», «А влечет В»; эквиваленция ― А↔В, читается: «А эквивалентно В», «А тогда и только тогда, когда В»; отрицание ― 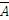, читается: «не А».

Отметим, что в русском языке один и тот же союз может употребляться в различных смыслах. Например, «или» ― в разделительном смысле и неразделительном, а в логике только в неразделительном. Использование логических операций строго в определенном смысле позволяет в математическом языке избавиться от неопределенности естественного языка, неоднозначности определений. Однако, как в естественном, так и в математическом языках, конъюнктивная, дизъюнктивная и т.п. связи могут быть выражены различными способами. Например:

1. «...Чиновник ― человек небогатый, но приличный».

2. «Мал золотник, да дорог».

3. «Последовательность ограничена, а предела не имеет».

4. «Функция непрерывна, однако не дифференцируема».

5. «Из дифференцируемости функций в точке х_о следует ее непрерывность в этой точке».

6. «Для того, чтобы функция была дифференцируема в точке х_о, необходимо, чтобы она была непрерывна в точке х_о» и т.п.

Рассмотрим два сложных предложения:

1. Если 9 делится на 2 и 3, то 8 делится на 5.

2. Если человек работает в вузе и преподает математику, то он имеет высшее образование.

Логическая структура этих сложных предложений одинакова. Если обозначить простые предложения буквами, а логические операции соответствующими символами, то каждое предложение можно заменить формулой (А&В)→ C. Эта формула выражает множество всех сложных высказываний, которые имеют такую же логическую структуру. Таким образом, буквы, входящие в формулу, играют роль своеобразных высказывательных переменных, принимающих в качестве своих значений «истина», «ложь».

Для того, чтобы узнать все возможные значения истинности, которые может принимать такая формула (а, следовательно, и значение истинности любого высказывания, имеющего данную форму) можно составить таблицу истинности этой формулы.

Например, для формулы (А&В)→ C таблица истинности имеет вид:

Как видим, формула имеет ложное значение только при одном набо­ре значений истинности высказывательных переменных, а при всех остальных наборах ― истинное значение.