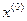Постановка задачи: дано уравнение
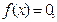 (1)
(1)
где функция 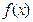 определена и непрерывна на заданном промежутке [ a,b ]. На эту функцию также могут накладываться дополнительные условия, например, дифференцируемость или монотонность. Требуется найти приближенные корни уравнения (1) на указанном отрезке с заданной точностью.
определена и непрерывна на заданном промежутке [ a,b ]. На эту функцию также могут накладываться дополнительные условия, например, дифференцируемость или монотонность. Требуется найти приближенные корни уравнения (1) на указанном отрезке с заданной точностью.
Задача решается в два этапа:
I. Отделение корней. Заданный промежуток [ a,b ] разбивается на отрезки, внутри каждого из которых находится один простой или кратный корень (1).
II. На отрезке, отделяющем корень, выбирается приближенное значение корня, иуточняется численными методами до тех пор, пока найденный корень не станет отличаться от истинного значения на величину, меньшую заданной погрешности.
Отделение корней производить графическим способом (реализовать программно) и, по возможности, аналитически, средствами математического анализа и алгебры. Для уточнения корней использовать следующие методы:
Метод половинного деления (дихотомия). Пусть на отрезке [ a0,b0 ] отделён корень уравнения (1). Процедура уточнения значения состоит в построении последовательности вложенных друг в друга отрезков [ ai,bi ] с убывающими длинами, каждый из которых содержит искомый корень уравнения (1). Для этого текущий k -ый сегмент [ ak,bk ] делится пополам и в качестве следующего, k+ 1 - го отрезка выбирается та половина, на концах которой функция 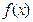 имеет разные знаки. Процесс прекращается, когда длина текущего отрезка становится меньше величины заданной погрешности. В качестве приближенного корня берется середина отрезка, полученного на последней итерации.
имеет разные знаки. Процесс прекращается, когда длина текущего отрезка становится меньше величины заданной погрешности. В качестве приближенного корня берется середина отрезка, полученного на последней итерации.
Метод хорд. Дополнительно предполагается, что функция 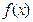 дважды непрерывно дифференцируема и знак
дважды непрерывно дифференцируема и знак 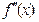 сохраняется на отрезке [ a,b ], отделяющем искомый корень.
сохраняется на отрезке [ a,b ], отделяющем искомый корень.
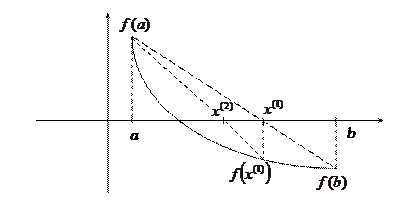
Рис.1. Метод хорд
Не теряя общности можно считать, что 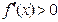 . Если
. Если 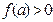 , то в качестве начального приближения к корню
, то в качестве начального приближения к корню 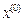 берётся b, а затем уточнения производятся по итерационной формуле (см. рис. 1)
берётся b, а затем уточнения производятся по итерационной формуле (см. рис. 1)
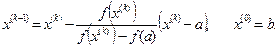 (2) В случае
(2) В случае 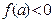 это соотношение принимает вид
это соотношение принимает вид
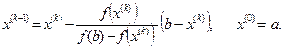 (3)
(3)
Итерации производятся до тех пор, пока величина
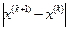
не станет меньше или равной заданной точности приближения. Тогда в качестве приближенного решения берётся 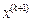 .
.
Метод простых итераций. Уравнение (1) эквивалентным преобразованием привести к виду
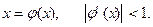 (4)
(4)
Условие, наложенное на производную, обеспечивает сходимость метода. Начальное приближение 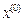 выбирается произвольным из отрезка, отделяющего корень. Уточнение значения корня производится по формуле
выбирается произвольным из отрезка, отделяющего корень. Уточнение значения корня производится по формуле
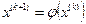 (5)
(5)
до тех пор пока величина
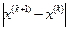
не станет меньше или равной заданной точности приближения. В качестве приближенного решения берётся 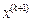 .
.
Преобразование уравнения (1) к виду (4) можно получить различными приёмами. Например, можно заменить (1) на равносильное уравнение
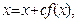
где c — константа, которую можно подобрать из условия
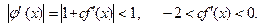
Метод Ньютона (метод касательных) требует следующих ограничений на функцию 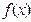 : дважды дифференцируемость;
: дважды дифференцируемость; 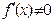 ; знакопостоянство
; знакопостоянство 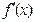 и
и 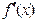 на отрезке, отделяющем корень. Начальное приближение
на отрезке, отделяющем корень. Начальное приближение 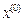 выбирается так, чтобы выполнялось условие
выбирается так, чтобы выполнялось условие 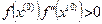 , итерации проводятся по формуле (см. рис. 2)
, итерации проводятся по формуле (см. рис. 2)
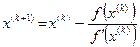 (6)
(6)
до тех пор пока величина 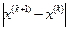 не станет меньше или равной заданной точности приближения. В качестве приближенного решения берётся
не станет меньше или равной заданной точности приближения. В качестве приближенного решения берётся 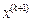 .
.
|



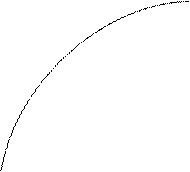

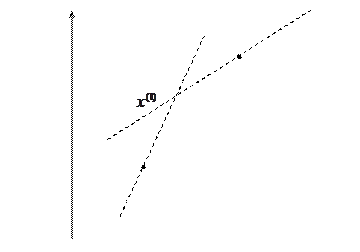
Рис.2. Метод Ньютона
Дополнительные вопросы:
1. Обосновать и вывести формулы (2)–(6), иллюстрируя вывод графически.
2. Для метода половинного деления получить оценку для количества итераций n, необходимых для достижения заданной точности решения 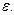
3. Уравнение Кеплера
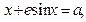
где 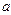 ,
, 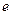 — константы,
— константы, 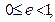 решить подходящим численным методом с заданной точностью, предварительно аналитически отделив корень.
решить подходящим численным методом с заданной точностью, предварительно аналитически отделив корень.
 2015-02-27
2015-02-27 748
748