Постановка задачи. Указанными ниже методами найти приближенные и точное решения системы линейных алгебраических уравнений (СЛАУ)
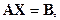 (1)
(1)
где матрица коэффициентов
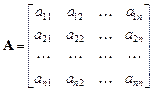
невырожденна, 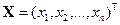 ,
, 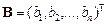 — вектор-столбцы неизвестных и свободных членов, с заданной точностью. Уклонение приближений к решению уравнения (1)
— вектор-столбцы неизвестных и свободных членов, с заданной точностью. Уклонение приближений к решению уравнения (1) 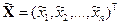 и
и 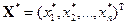 друг от друга оценивать в метрике
друг от друга оценивать в метрике
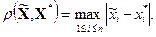
Найденные приближенные решения сравнить с точным решением системы (1), полученным методом последовательного исключения неизвестных Гаусса.
Перед решением СЛАУ требуется проанализировать (анализ нужно включить в программу):
1) Если 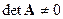 — решение существует и единственно. Однако, при большом числе обусловленности матрицы
— решение существует и единственно. Однако, при большом числе обусловленности матрицы 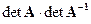 (ориентировочно > 103) решение, в том числе и «точным» алгоритмом Гаусса, может быть неустойчиво к ошибкам округления. В этом случае задача является некорректной, для её решения нужны специальные методы, которые здесь не рассматриваются.
(ориентировочно > 103) решение, в том числе и «точным» алгоритмом Гаусса, может быть неустойчиво к ошибкам округления. В этом случае задача является некорректной, для её решения нужны специальные методы, которые здесь не рассматриваются.
2) Если же определитель равен нулю
a) и расширенную матрицу системы (1) можно преобразовать к виду, когда как минимум одна строка её коэффициентов — нули, то решений бесконечно много;
b) иначе — система не совместна, решения не существует.
Метод Гаусса. Идея метода состоит в последовательном исключении неизвестных из СЛАУ. Из первого уравнения системы (1) находим
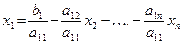 .
.
Подставим выражение для 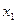 во все остальные уравнения системы, начиная со второго:
во все остальные уравнения системы, начиная со второго:
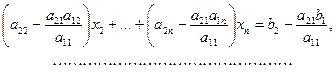
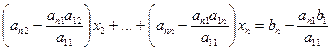
Для расширенной матрицы коэффициентов это означает, что каждый элемент первой строки следует поделить на диагональный элемент, а все остальные строки преобразовать, как показано выше. После этого все коэффициенты первого столбца, лежащие ниже главной диагонали, будут равны нулю. Затем аналогичная процедура проводится со второй строкой матрицы и ниже её лежащими строками. И так далее до тех пор, пока все элементы расширенной матрицы, лежащие ниже главной диагонали, не станут равны нулю. После приведения матрицы к треугольному виду находятся все неизвестные, начиная с 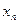 , которое фактически уже было определено.
, которое фактически уже было определено.
Для уменьшения погрешности вычислений метода Гаусса нужно, чтобы на главной диагонали матрицы стояли максимальные по модулю значения коэффициентов. Этого можно добиться, например, переставляя соответствующим образом строки. Такая процедура называется выбором главного элемента и осуществляется в алгоритме Гаусса всякий раз при переходе к новой строке.
Метод простых итераций. Систему (1) эквивалентным преобразованием привести к виду
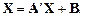 (2)
(2)
Начальное приближение 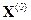 можно выбирать произвольно, но обычно для него используется нуль-вектор или столбец свободных членов. Итерации проводятся по формуле
можно выбирать произвольно, но обычно для него используется нуль-вектор или столбец свободных членов. Итерации проводятся по формуле
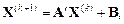
до тех пор пока величина 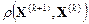 не станет меньше или равной заданной погрешности, тогда в качестве приближенного решения выбирается
не станет меньше или равной заданной погрешности, тогда в качестве приближенного решения выбирается 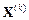 или
или 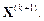
Достаточное условие сходимости метода итераций:
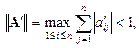
причем чем меньше норма 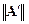 , тем быстрее сходимость.
, тем быстрее сходимость.
Условие сходимости также выполняется при диагональном преобладании в матрице 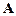 , когда абсолютные величины диагональных элементов матрицы больше суммы модулей всех недиагональных элементов соответствующей строки.
, когда абсолютные величины диагональных элементов матрицы больше суммы модулей всех недиагональных элементов соответствующей строки.
Преобразование системы (1) к виду (2) с матрицей 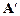 , удовлетворяющей условию сходимости, может быть выполнено различными способами. Например, можно переставить уравнения системы (1) так, чтобы матрица коэффициентов имела диагональное преобладание, а затем разрешить каждое i- ое уравнение относительно i– ой неизвестной.
, удовлетворяющей условию сходимости, может быть выполнено различными способами. Например, можно переставить уравнения системы (1) так, чтобы матрица коэффициентов имела диагональное преобладание, а затем разрешить каждое i- ое уравнение относительно i– ой неизвестной.
Метод Зейделя отличается от метода простых итераций тем, что найденное приближение для неизвестного сразу же используется для отыскания следующих переменных:
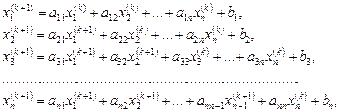
что обычно приводит к более быстрой сходимости итерационного процесса. Достаточные условия сходимости этого метода такие же, как в методе простых итераций.
Дополнительные вопросы:
1. Сколько арифметических операций требуется для решения СЛАУ из n уравнений с n неизвестными методом Гаусса?
2. Определитькоэффициенты системы (1) при n = 2 так, чтобы достаточные условия сходимости метода простых итераций не выполнялись, но, тем не менее, итерационный процесс сходился.
3. Найти решения двух плохо обусловленных СЛАУ
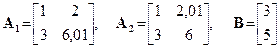
всеми вышеуказанными методами. Почему решения этих близких систем так сильно отличаются друг от друга?
4. Перечислите преимущества и недостатки каждого из используемых в лабораторной работе методов.
 2015-02-27
2015-02-27 753
753








