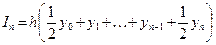2015-02-27
401
(4)
Формула Симпсона. Число разбиений здесь четно.
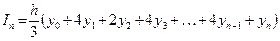(5)
Для достижения заданной точности использовать метод двойного пересчета: после вычисления интеграла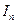 
по формуле (4) или (5) с числом разбиений 
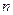, рассчитывается 
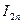с двойным количеством разбиений и проверяется неравенство
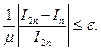(6)
Если оценка (6) не выполняется, то число разбиений снова удваивают, до тех пор, пока неравенство не станет истинным. Для метода трапеций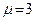 
, для формулы Симпсона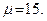 
Интегрирование методом Монте-Карло. Пусть значения подынтегральной функции заключены на отрезке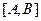 
(например можно взять 
, 
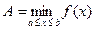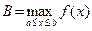). Вместо равномерного разбиения (2) построим точки
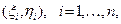(7)
где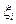 
— случайное число, равномерно распределённое на сегменте 
, 
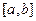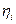— случайное число, равномерно распределённое на отрезке 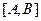. Тогда, при достаточно большом ,
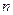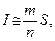(8)
где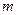 
— количество точек (7), лежащих ниже подынтегральной кривой, 
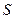— площадь прямоугольника 
.
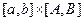Дополнительные вопросы:
1. Вывести формулы трапеций и Симсона, дать их геометрическую интерпретацию. Каков порядок точности формул (4), (5)?
2. Обосновать метод двойного пересчета, вывести неравенство (6).
3. Обосновать метод Монте-Карло, дать его геометрическую интерпретацию.
4. Обобщить метод Монте-Карло на случай двойных и, вообще, кратных интегралов.
