Кроме проверки на совпадение или несовпадение состояний порядковая шкала позволяет их сравнивать, т.е. больше-меньше, больше или равно – меньше или равно, в результате чего возможно установление приоритетов. Отношение порядка не задает «дистанции» между сравниваемыми классами. Если в шкале наименований было безразлично, в каком порядке мы расположим классификационные градации шкалы, то в порядковой шкале они образуют последовательность от градации «самое малое значение» к градации «самое большое значение» (или наоборот).
Иногда число градаций в шкале задается заранее, и эксперимент лишь определяет, к какому из упорядоченных классов относится наблюдаемый признак (сила землетрясения, воинское звание …) В других случаях эталонные классы отсутствуют, а упорядочение проводится непосредственным парным сравнением самих изучаемых объектов (выстраивание в шеренгу по росту, определение мест в результате спортивного соревнования …)
Даже если экспериментальные данные представлены цифрами, их нельзя рассматривать как числа. Над ними нельзя производить арифметические операции. При обработке данных, измеренных в порядковой шкале, можно вычислять ранг и производить те же преобразования, что и в случае номинальной шкалы.
Для порядковой шкалы кроме трех аксиом эквивалетности результаты измерений должны удовлетворять еще двум аксиомам упорядоченности:
4) если А≠В, то либо А>B, либо B<A;
5) если A>B и B>C, то A>C.
Использование порядковой шкалы позволяет присваивать ранги объектам по какому-либо признаку. Надо решить, кто получает первый ранг: объект с самой большей степенью выраженности какого-либо качества или наоборот. Чаще всего это абсолютно безразлично и не отражается на конечном результате. Традиционно принято первый ранг приписывать объектам с большей степенью выраженности качества (большему значению – меньший ранг). Например, чемпиону присуждают первое место. Правило связанных рангов. Объектам с одинаковой выраженностью свойств приписывается один и тот же ранг. Этот ранг представляет собой среднее значение тех рангов, которые они получили бы, если бы не были равны. Например, надо проранжировать выборку, содержащую ряд одинаковых метрических данных: {4, 5, 9, 2, 6, 5, 9, 7, 5, 12}. После упорядочивания выборки следует вычислить среднее арифметическое значение связанных рангов. В соответствии с этим правилом сумма всех присвоенных рангов для группы численностью N должна равняться N(N+1)/2, вне зависимости от наличия или отсутствия связей в рангах.
| Метрические данные | Предварительное ранжирование | Окончательное ранжирование |
| (2+3)/2=2,5 | ||
| (2+3)/2=2,5 | ||
| (6+7+8)/3=7 | ||
| (6+7+8)/3=7 | ||
| (6+7+8)/3=7 | ||
Кроме моды можно рассчитать медиану Me. Медиана, по сути, делит ранжированный ряд пополам, т.е. 50% оценок находятся до этого значения, а 50% - после этого значения. Пусть, например, 10 экспертов дали измеряемому свойству объекта оценку, равную 1 баллу; 15 экспертов – оценку 2 балла; 20 экспертов – оценку 3 балла и 5 экспертов – оценку 4 балла. Всего было привлечено к экспертизе 10+20+15+5=50 экспертов (табл.)
| Оценка | ||||
| Число экспертов, давших оценку | ||||
| Относительная чистота, % |
Медиана в этом случае равна 2 баллам, т.к. именно для этой оценки характерна граница в 50% ответов. Мода равна 3.
Можно разбивать всю выборку на части в любой пропорции и находить выборочные квантили уровня p, 0<p<1.
Т.к. оценки каждого из показателей упорядочены, то можно анализировать, насколько эти порядки, например, двух показателей совпадают или отличаются друг от друга. Тем самым можно говорить о взаимосвязанности факторов. Эти процедуры осуществляются с помощью вычисления корреляции рангов методом Спирмена или Кендалла. Эти ранговые корреляции показывают наличие или отсутствие связей в двух рядах признаков, измеренных упорядоченными шкалами.
Если проранжированные показатели свойств Xi и Yi i-го объекта имеют один и тот же диапазон рангов от 1 до n, то коэффициент ранговой корреляции Спирмена будет вычисляться по формуле:

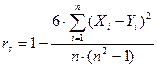
Если этот коэффициент по модулю близок к единице, то говорят о сильной линейной взаимосвязи между этими показателями, если он близок по модулю к нулю, то это свидетельствует об отсутствии линейной взаимосвязи.
Если имеются «связанные ранги», то применяется коэффициент ранговой корреляции Кендалла:
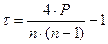
Здесь Р – число совпадений для пар рангов. Например, первым экспертом товару А дан ранг 1, а товару Б – ранг 3. Нужно еще посмотреть, сколько еще экспертов дают товару А более высокий ранг, чем товару Б. Это и есть число совпадений.
 2015-02-27
2015-02-27 1896
1896
