|
 Для решения задачи применим метод Гаусса. Из условия следует, что заряд, сообщенный листу стекла извне (его принято называть свободным зарядом) распределен в пространстве симметрично относительно плоскости, проходящей через точку А перпендикулярно оси х (см. рис.1.8). Поэтому есть основание утверждать, что электрическое поле симметрично относительно этой плоскости. Кроме того, так как мы рассматриваем диэлектрик, находящийся в электрическом поле, то чтобы исключить рассмотрение влияния поляризационных зарядов диэлектрика, теорему Гаусса следует применять для вектора электрического смещения
Для решения задачи применим метод Гаусса. Из условия следует, что заряд, сообщенный листу стекла извне (его принято называть свободным зарядом) распределен в пространстве симметрично относительно плоскости, проходящей через точку А перпендикулярно оси х (см. рис.1.8). Поэтому есть основание утверждать, что электрическое поле симметрично относительно этой плоскости. Кроме того, так как мы рассматриваем диэлектрик, находящийся в электрическом поле, то чтобы исключить рассмотрение влияния поляризационных зарядов диэлектрика, теорему Гаусса следует применять для вектора электрического смещения  . Полагая, что точки А,В,С достаточно удалены от краев листа стекла, можно считать, что линии вектора
. Полагая, что точки А,В,С достаточно удалены от краев листа стекла, можно считать, что линии вектора 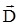 в любой точке расположены параллельно оси х. Исходя из этого, будем выбирать гауссову поверхность в виде цилиндра, образующие которого параллельны оси х, а основания перпендикулярны к ней и расположены от плоскости симметрии на равном расстоянии.
в любой точке расположены параллельно оси х. Исходя из этого, будем выбирать гауссову поверхность в виде цилиндра, образующие которого параллельны оси х, а основания перпендикулярны к ней и расположены от плоскости симметрии на равном расстоянии. Начало координат оси х расположим в точке А.
Разобьем пространство на две области:
 1.
1. 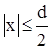 . Поток вектора электрического смещения через выбранную поверхность
. Поток вектора электрического смещения через выбранную поверхность
равен 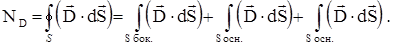
Первый интеграл равен нулю, так как линии вектора 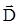 не пересекают боковую поверхность цилиндра. Второй и третий интегралы равны по признаку симметрии.
не пересекают боковую поверхность цилиндра. Второй и третий интегралы равны по признаку симметрии.
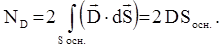
Свободный заряд, попавший внутрь выбранной поверхности, равен
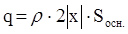 .
.
По теореме Гаусса
|
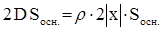 .
. Отсюда 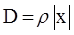 внутри листа стекла.
внутри листа стекла.
Известно, что в том случае, когда диэлектрик полностью заполняет пространство между двумя эквипотенциальными поверхностями, связь между электрическим смещением и напряженностью поля выражается весьма просто:
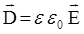 .
.
Это же справедливо и для модулей векторов. Тогда напряженность электрического поля внутри стекла равна 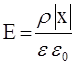 .
.
2. 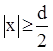 . Поток вектора электрического смещения через поверхность цилиндра, как и в предыдущем случае выражается формулой
. Поток вектора электрического смещения через поверхность цилиндра, как и в предыдущем случае выражается формулой 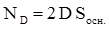 .
.
Свободный заряд, попавший внутрь гауссовой поверхности, в этом случае равен
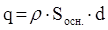 .
.
По теореме Гаусса 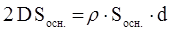 .
.
 Тогда
Тогда 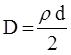 , а напряженность, соответственно
, а напряженность, соответственно 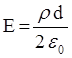 , так как вне стекла e = 1. Таким образом, вне листа стекла поле является однородным, его напряженность не зависит от координат.
, так как вне стекла e = 1. Таким образом, вне листа стекла поле является однородным, его напряженность не зависит от координат.
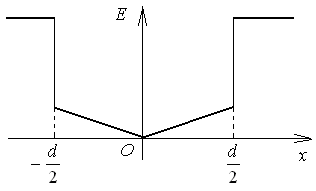
|
|
модуля вектора напряженности от координаты х (рис.1.9).
Отметим, что при переходе из стекла в воздух модуль напряженности скачком увеличивается в e раз.
Найдем теперь численные значения напряженности Е в точках А,В,С (рис.1.9).
1. Точка А: х = 0; ЕА = 0.
2. Точка В: х = d/4; 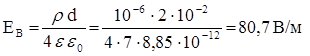 .
.
3. Точка С: х = d/2; ЕС имеет два значения:
а) внутри стекла 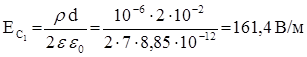 ;
;
б) вне стекла 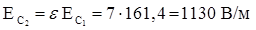 .
.
Ответ: ЕА = 0; ЕВ = 80,7 В/м; ЕС1 = 161,4 В/м, ЕС2 = 1130 В/м.
Пример 5. Эбонитовый сплошной шар (e = 3) радиуса R = 5 см несет заряд, равномерно распределенный с объемной плотностью r = 10 нКл/м3. Определить напряженность электрического поля в точках: 1) на расстоянии r1 = 3 см от центра шара; 2) на поверхности шара; 3) на расстоянии r3 = 10 см от центра шара. Построить график зависимости Е(r).
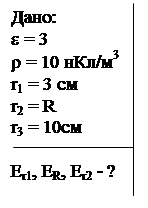
 2015-02-27
2015-02-27 1344
1344








