Решение. Применим метод Гаусса. Как и в предыдущей задаче, теорему Гаусса надо применять для вектора электрического смещения

Применим метод Гаусса. Как и в предыдущей задаче, теорему Гаусса надо применять для вектора электрического смещения 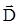, так как в этом случае достаточно учесть только дополнительные (свободные) заряды, сообщенные диэлектрику извне и не надо рассматривать связанные поляризационные заряды диэлектрика. Ввиду сферически симметричного распределения свободного заряда есть основание утверждать, что линии вектора 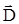в любой точке направлены вдоль радиусов, проведенных из точки О, и модуль D имеет одинаковое значение на равных расстояниях от центра шара О. Следовательно, в качестве гауссовых поверхностей следует выбирать сферы радиуса r с центром в точке О (рис.1.10).

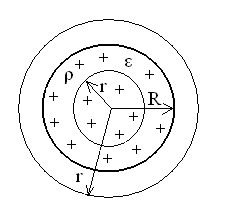Рассмотрим две области пространства:

Рис.1.10

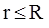1. . Поток вектора электрического смещения через гауссову сферу равен

.

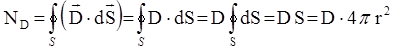Свободный заряд, попавший внутрь этой сферы, равен .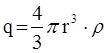

По теореме Гаусса 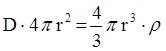, отсюда .

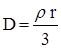Так как и в этом примере диэлектрик заполняет пространство между двумя эквипотенциальными поверхностями, то связь между 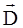и 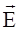имеет вид

.

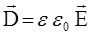Тогда модуль напряженности электрического поля равен .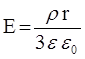

2. 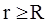. Поток вектора электрического смещения через сферу радиуса r, как и в предыдущем случае, равен .

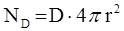Свободный заряд, попавший внутрь этой сферы с r > R – это весь заряд шара:

.

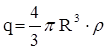По теореме Гаусса 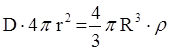, отсюда

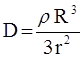, а напряженность поля в этой области 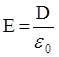, так как e = 1.

Получим .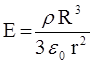

Теперь можно построить график зависимости E(r) (рис.1.11).

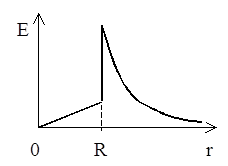
Отметим, что на границе перехода поля из эбонита в воздух происходит скачок напряженности в e раз.

Вычислим значения напряженности в нужных точках:

1) r₁ = 3 см. .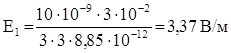

Рис.1.11

2) r₂ = R. Напряженность имеет два значения:

а) внутри шара ;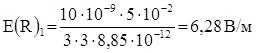

б) вне шара .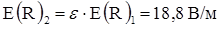

3) r₃ = 10 см. .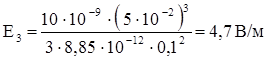

Ответ: Е₁ = 3,37 В/м; Е(R)₁ = 6,28 В/м, Е(R)₂ = 18,8 В/м; Е₃ = 4,7 В/м.

Пример 6. Сплошной парафиновый шар (e = 2) радиусом R =10 см равномерно заряжен с объемной плотностью r = 1 мкКл/м³. Определить потенциал электрического поля в центре шара и на его поверхности. Построить график зависимости j (r).

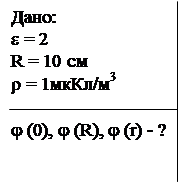Решение

Воспользуемся связью между напряженностью и потенциалом электростатического поля .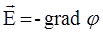

Для поля со сферической симметрией, каким является поле шара, это соотношение можно записать в виде 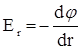, где E_r – проекция вектора напряженности на радиус – вектор , проведенный из центра шара. В нашем случае E_r = E, то есть модулю вектора напряженности.

Тогда разность потенциалов двух точек поля может быть найдена интегрированием

.

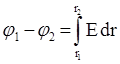Для нахождения численного значения потенциала необходимо задать нулевой уровень потенциала. В данном случае нулевой уровень удобнее всего задать в бесконечности.

Тогда 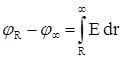, где j_R – потенциал на поверхности шара.

Учтем, что , а выражение для напряженности поля в пространстве, окружающем шар, возьмем из предыдущей задачи .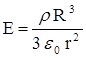

Тогда .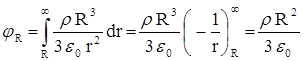

Разность потенциалов между центром шара и его поверхностью найдем таким же способом 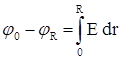, где j₀ – потенциал в центре шара.

Тогда 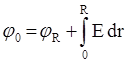, а напряженность поля внутри шара опять возьмем из предыдущей задачи: 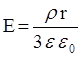. Найдем j₀:

.

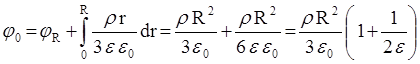Нарисуем график зависимости j (r) (рис.1.12).

Рис.1.12

Найдем численные значения потенциалов на поверхности шара j_R и в его центре j₀.

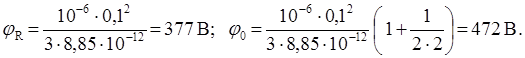
Ответ: j_R = 377 В, j₀ = 472 В.