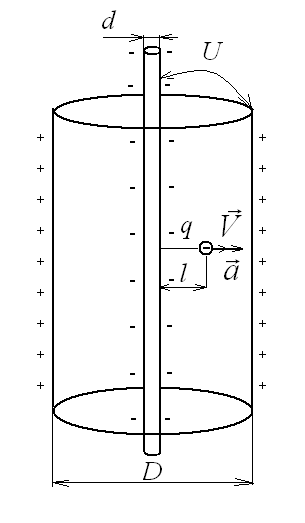
 Ускорение электрона можно найти из второго закона Ньютона, но для этого надо знать силу, действующую на электрон. Сила, действующая на заряд, находящийся в электрическом поле, как известно, равна F = |q|E, значит, необходимо найти напряженность электрического поля между катодом и анодом. Так как катод представляет собой тонкую нить, воспользуемся формулой для напряженности поля, созданного тонкой заряженной нитью с линейной плотностью заряда τ.
Ускорение электрона можно найти из второго закона Ньютона, но для этого надо знать силу, действующую на электрон. Сила, действующая на заряд, находящийся в электрическом поле, как известно, равна F = |q|E, значит, необходимо найти напряженность электрического поля между катодом и анодом. Так как катод представляет собой тонкую нить, воспользуемся формулой для напряженности поля, созданного тонкой заряженной нитью с линейной плотностью заряда τ.
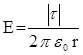 , где r – расстояние от оси нити. Для нахождения τ воспользуемся связью между напряженностью и разностью потенциалов электростатического поля. В данном случае
, где r – расстояние от оси нити. Для нахождения τ воспользуемся связью между напряженностью и разностью потенциалов электростатического поля. В данном случае
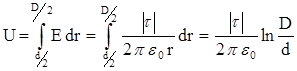 .
.
|
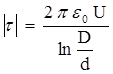 и модуль
и модуль напряженности поля равен 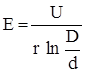 .
.
Теперь по второму закону Ньютона 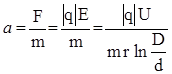 .
.
Рассчитаем ускорение электрона, учитывая, что
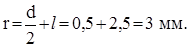
|
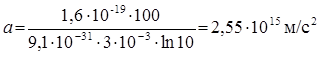 .
. Для нахождения скорости электрона воспользуемся связью работы и кинетической энергии. По теореме о кинетической энергии приращение кинетической энергии тела равно суммарной работе всех сил, действующих на тело: ΔWк = Aвсех сил. В этом случае на электрон действует только сила электрического поля, а начальная скорость электрона по условию мала, поэтому
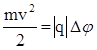 ,
,
где Δφ – разность потенциалов между катодом и точкой, в которой находится электрон. Отсюда 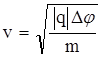 .
.
Разность потенциалов найдем, используя связь напряженности поля и разности потенциалов:
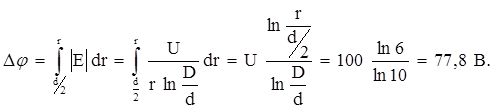
И, наконец, рассчитаем скорость электрона
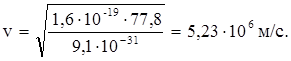
Ответ: а = 2,55·1015 м/с2, v = 5,23·106 м/с.
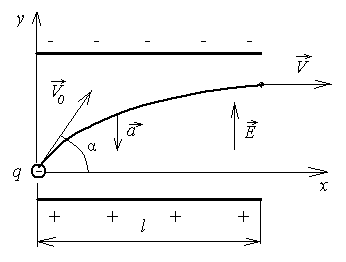
Пример 2. Электрон влетает в поле плоского конденсатора со скоростью v0 = 1 Мм/с под углом α = 30о к его пластинам. Длина пластин l = 5 см. Найти напряженность поля, при которой скорость электрона при вылете из конденсатора будет направлена параллельно его пластинам.

Дано: α = 30о l = 5 см |q| = 1,6·10-19 Кл m = 9,1·10-31 кг v0 = 1 Мм/с E -?
Решение
|
Поле плоского конденсатора является однородным, поэтому на электрон в этом поле будет действовать постоянная сила, а значит движение электрона будет равноускоренным. Для описания этого движения выберем начало координат в точке влета электрона, направим ось х вдоль пластин, а ось у – перпендикулярно им (рис.2.2). Тогда закон движения электрона примет вид 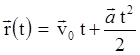 . Скорость электрона при этом равна
. Скорость электрона при этом равна 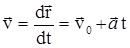 . Запишем эти уравнения в проекциях на выбранные оси координат:
. Запишем эти уравнения в проекциях на выбранные оси координат:
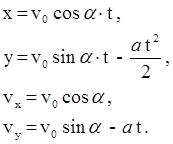
Так как в точке вылета x = l, то 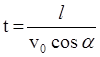 , а так как электрон вылетает параллельно пластинам, то в точке вылета vy = 0, тогда
, а так как электрон вылетает параллельно пластинам, то в точке вылета vy = 0, тогда 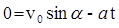 . Отсюда
. Отсюда
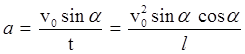 .
.
По второму закону Ньютона 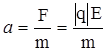 , отсюда
, отсюда 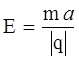 .
.
Тогда окончательно получаем
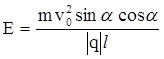 .
.
Вычислим напряженность поля: 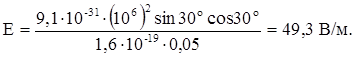
Ответ: Е = 49,3 В/м.
Пример 3. Пространство между пластинами плоского конденсатора заполнено диэлектриком. Расстояние между пластинами d = 2 мм. На пластины подана разность потенциалов U1 = 600 В. Если, отключив источник напряжения, вынуть диэлектрик из конденсатора, то разность потенциалов на пластинах возрастет до U2 = 1800 В. Найти поверхностную плотность связанных зарядов на диэлектрике σсв и диэлектрическую восприимчивость κ диэлектрика.
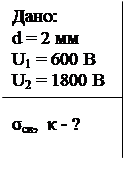
 2015-02-27
2015-02-27 1570
1570
