Основное содержание темы

Моделирование процесса функционирования ГПС в настоящее время сводится к построению главным образом математических моделей отдельных аспектов этого процесса.

Поток вызовов - последовательность сообщений о пожарах и других чрезвычайных ситуациях поступающих одно за другим в какие-то случайные моменты времени на ЦППС города.

Процесс поступления вызовов пожарных подразделений любого города протекает неравномерно и носит вероятностный характер.

Основной характеристикой потока вызовов пожарных подразделений является интенсивность (или плотность) потока l, равная среднему числу событий (вызовов пожарных подразделений), возникающих в единицу времени.

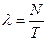(вызовов/ед.времени) (1)

где: N - число вызовов в исследуемом периоде времени; Т - исследуемый период времени.

Математической моделью простейшего потока событий, описывающий распределение вероятностей возникновения того или иного числа событий на интервале времени определённой длительности, может явиться закон Пуассона. В соответствии с этим законом вероятность Рk₍_t₎ того, что на интервале времени t возникает ровно k событий, вычисляется по формуле:

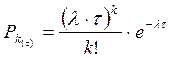(k=0,1,2,3,...) (2)

где: k - число вызовов в интервале времени t; k! - факториал от числа вызовов за интервал времени; t - интервал времени (t = 1 сутки)

Для интервала времени фиксированной длительности t вероятности Рk₍_t₎ (k = 0,1,2,3,...) связаны между собой соотношением:

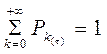(3)

Эмпирическая вероятность того или иного k событий в течении суток вычисляется по формуле:

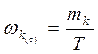(4)

где: m _k - число суток с указанным числом выездов;

Определение теоретического распределения числа суток с тем или иным числом вызовов пожарных подразделений в течении анализируемого периода времени Т определяется по формуле:

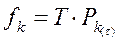(5)

При выполнении задания требуется проверить гипотезу о том, что эмпирическое распределение числа суток с тем или иным числом вызовов пожарных подразделений носит пуассоновский характер.

Определение степени близости полученного эмпирического распределения к Пуассоновскому производится при помощи критерия согласия Романовского R, который позволят определить, являются ли имеющиеся между распределениями расхождения случайными или закономерными, который вычисляется по формуле (6)

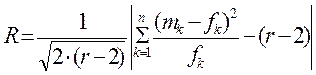(6)