Из первых двух фундаментальных законов механики – баланса количества движения и момента количества движения следует, что необходимыми условиями равновесия тела в инерциальной системе отсчета является равенство нулю главного вектора и главного момента внешних воздействий:
 ; (2.5)
; (2.5)
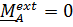 . (2.6)
. (2.6)
В проекции на оси декартовой системы координат векторные уравнения (2.5) и (2.6) представляют собой в общем случае систему шести уравнений равновесия:
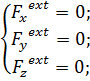
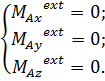 (2.7)
(2.7)
Для так называемой плоской системы сил, когда все силы лежат в одной плоскости 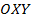 , а моменты, разумеется, ей перпендикулярны, система состоит из трех уравнений
, а моменты, разумеется, ей перпендикулярны, система состоит из трех уравнений
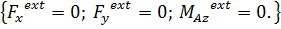 (2.8)
(2.8)
Моментом силы относительно оси 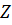 называется проекция на эту ось момента, вычисленного относительно любой точки на этой оси:
называется проекция на эту ось момента, вычисленного относительно любой точки на этой оси: 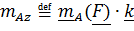 . Действительно, умножая скалярно на орт оси
. Действительно, умножая скалярно на орт оси 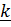 равенство
равенство
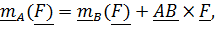
получим 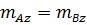 . Раскладывая силу на составляющие
. Раскладывая силу на составляющие 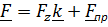 , получим практическое правило для вычисления момента относительно оси:
, получим практическое правило для вычисления момента относительно оси:
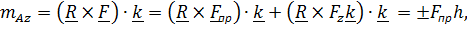
где знак (+) в том случае, если при взгляде с оси 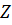 составляющая силы
составляющая силы 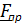 стремится повернуть тело против часовой стрелки, и знак
стремится повернуть тело против часовой стрелки, и знак 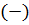 – по часовой стрелке (рис. 2.2).
– по часовой стрелке (рис. 2.2).
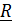 |
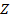 |
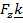 |
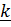 |
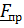 |
| h |
| A |
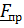 |
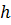 |
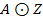 |
| Рис. 2.2. Момент силы относительно оси |
 2015-02-04
2015-02-04 707
707








