Приведем тождества, которые будут использоваться в дальнейшем. Первое из них, не связанное, правда, с определителем, имеет вид: (1.7)
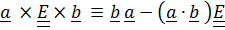 ; (1.13)
; (1.13)
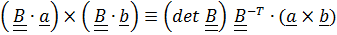 ; (1.14)
; (1.14)
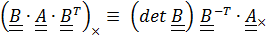 ; (1.15)
; (1.15)
 . (1.16)
. (1.16)
Тождество (1.14) следует из определения определителя (1.11). Перепишем его в виде:  ,
,
и поскольку вектор 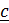 – любой, то
– любой, то
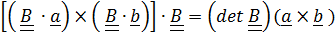 .
.
Умножив это равенство скалярно на 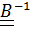 справа, приходим к (1.14).
справа, приходим к (1.14).
Тождество (1.15) линейно относительно  , поэтому можно взять в качестве
, поэтому можно взять в качестве  одну диаду
одну диаду 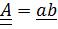 . Левая часть примет вид:
. Левая часть примет вид:
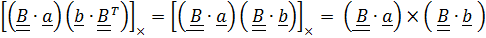 ,
,
и по тождеству (1.14) с учетом того, что 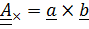 получаем (1.15).
получаем (1.15).
Тождество (1.16) получается из (1.15).
«Несущественная» часть 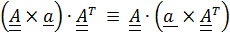 доказывается, если переписать ее в виде
доказывается, если переписать ее в виде 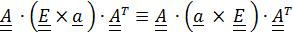 .
.
Так как тензор 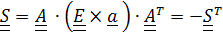 кососимметричный, представим его в виде
кососимметричный, представим его в виде 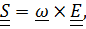 где
где 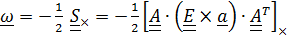 по тождеству (1.15) с учетом того, что
по тождеству (1.15) с учетом того, что 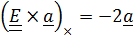 равен
равен 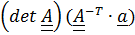 .
.
 2015-02-04
2015-02-04 912
912








