Ортогональные тензоры. Тензор поворота

Тензор 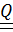называется ортогональным, если он удовлетворяет уравнению 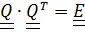, или, вспоминая определение обратного тензора .

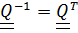Пусть векторы 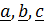преобразуются тензором 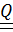в = , = , = .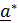

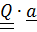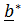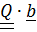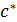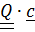Скалярное произведение 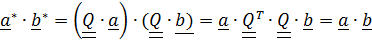не изменяется, т. е. не изменяются ни длины векторов, ни углы между ними.

Вычисляя определитель от 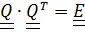, получим , .

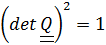Из определения 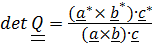следует, что если 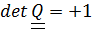, то ориентация троек векторов не изменяется, т.е. они поворачиваются как жесткая система и поэтому такой тензор называется тензором поворота. Если же определитель равен ( 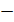1), то поворот сопровождается центральной инверсией 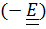, изменяющей направления всех векторов на противоположные.