Дифференцируя основную формулу кинематики твердого тела (4.3)
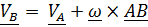 , получаем формулу для ускорений:
, получаем формулу для ускорений:
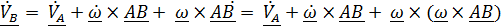 .
.
Производная вектора угловой скорости по времени называется вектором углового ускорения 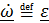 , слагаемое
, слагаемое 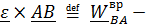 вращательное ускорение точки В вокруг полюса А,
вращательное ускорение точки В вокруг полюса А, 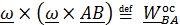 – осестремительное ускорение. Таким образом
– осестремительное ускорение. Таким образом
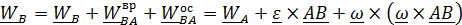 (4.6)
(4.6)
Формула (4.6) справедлива, разумеется, для произвольного движения.
Поясним термин «осестремительное ускорение». В теоретической механике линия, проходящая через полюс А параллельно вектору угловой скорости 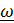 ,называется мгновенной осью вращения, поскольку вращательная скорость
,называется мгновенной осью вращения, поскольку вращательная скорость 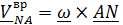 всех точек
всех точек 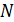 на этой оси равна нулю. Нетрудно убедиться, что двойное векторное произведение
на этой оси равна нулю. Нетрудно убедиться, что двойное векторное произведение 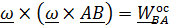 направлено к мгновенной оси вращения под прямым углом, а его модуль равен:
направлено к мгновенной оси вращения под прямым углом, а его модуль равен:
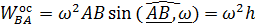 ,
,
где h – расстояние от точки В до мгновенной оси вращения (рис. 4.3,a).
| Рис. 4.3. Ускорения точек твердого тела
|
Для плоского движения (рис. 4.3,б) мгновенная ось вращения на плоском рисунке вырождается в точку – «центр», поэтому во многих учебниках 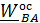 называют «центростремительным»
называют «центростремительным» 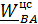 . Векторы угловой скорости
. Векторы угловой скорости 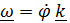 и углового ускорения
и углового ускорения 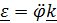 перпендикулярны плоскости движения. Раскрывая двойное векторное произведение, получим:
перпендикулярны плоскости движения. Раскрывая двойное векторное произведение, получим:
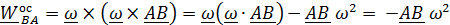 , так как
, так как 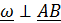 .
.
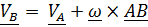 , получаем формулу для ускорений:
, получаем формулу для ускорений: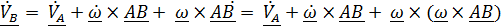 .
.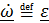 , слагаемое
, слагаемое 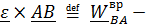 вращательное ускорение точки В вокруг полюса А,
вращательное ускорение точки В вокруг полюса А, 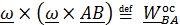 – осестремительное ускорение. Таким образом
– осестремительное ускорение. Таким образом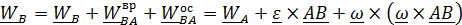 (4.6)
(4.6)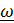 ,называется мгновенной осью вращения, поскольку вращательная скорость
,называется мгновенной осью вращения, поскольку вращательная скорость 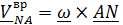 всех точек
всех точек 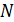 на этой оси равна нулю. Нетрудно убедиться, что двойное векторное произведение
на этой оси равна нулю. Нетрудно убедиться, что двойное векторное произведение 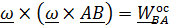 направлено к мгновенной оси вращения под прямым углом, а его модуль равен:
направлено к мгновенной оси вращения под прямым углом, а его модуль равен: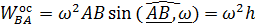 ,
,
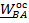
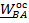
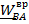
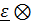
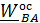 называют «центростремительным»
называют «центростремительным» 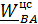 . Векторы угловой скорости
. Векторы угловой скорости 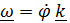 и углового ускорения
и углового ускорения 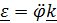 перпендикулярны плоскости движения. Раскрывая двойное векторное произведение, получим:
перпендикулярны плоскости движения. Раскрывая двойное векторное произведение, получим: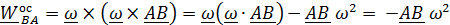 , так как
, так как 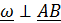 .
. 2015-02-04
2015-02-04 408
408








