2015-02-04
587
Как уже отмечалось в разд. (4.1.1), положение твердого тела можно описать вектором положения какой-либо точки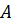 
, называемой полюсом, и ориентацией, которую удобно описывать с помощью жестко связанной с телом тройки векторов. Для простоты возьмем ортонормированную тройку векторов, которые в отсчетном положении обозначаются 
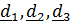, а в актуальном – 
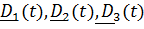. В качестве отсчетного положения чаще всего удобно взять положение в момент времени 
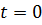, тогда 
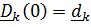, но иногда в качестве отсчетного удобнее взять положение, которое тело никогда не занимало в прошлом и, возможно, никогда не займет в будущем. Так, например, можно принять, что 
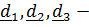орты декартовой системы координат в используемой системе отсчета.
Разложим векторы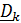 
по базису 
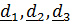(рис. 4.4):
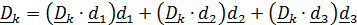
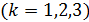. (4.7)
Скалярные произведения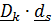 
, равные косинусам углов между 
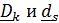, называются направляющими косинусами: 
.
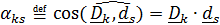Применяя правило суммирования по повторяющимся индексам, вместо трех строчек (4.7), в каждой из которых три слагаемых, можно написать короткую формулу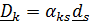 
. При этом принимается соглашение, что по индексам, присутствующим в обеих частях равенства (в данном случае это индекс 
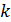) суммирование не производится, а равенство повторяется 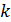раз.
Из девяти направляющих косинусов только три являются независимыми, поскольку между ними есть шесть уравнений связей:
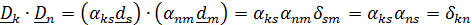, (4.8)
где, напомним,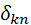 
называется символом Кронекера.
В формуле (4.8) символ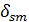 
«отфильтровал» в двойной сумме по индексам 
только те слагаемые, у которых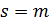 
.
Знание направляющих косинусов полностью решает задачу описания движения, но выбрать три независимых и аналитически выразить через них остальные шесть невозможно, так как система уравнений (4.8) нелинейная, поэтому в качестве трех параметров, задающих ориентацию тела, обычно используются углы.
