Пусть твердое тело вращается вокруг неподвижной оси под действием момента 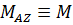 (рис. 5.15а).
(рис. 5.15а).
| Рис. 5.15. Динамические реакции |
 y y |
 y y |
Поскольку нас интересуют только реакции, возникающие при вращении тела (динамические реакции), прочие воздействия не рассматриваются. Уравнения первого и второго законов имеют вид:
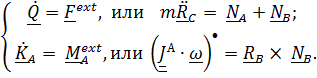 (5.36)
(5.36)
Найдем проекции (5.36) на оси 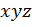 , связанные с телом:
, связанные с телом:
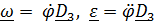 ,
, 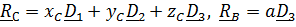 ;
;
 ;
;
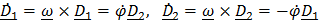 ;
;
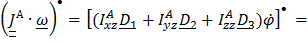
 ;
;
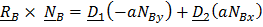 ;
;
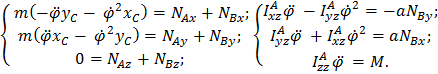 (5.37)
(5.37)
Последнее уравнение – уравнение вращения вокруг неподвижной оси, третье уравнение содержит только сумму реакций, но не позволяет их найти. Первое, второе, четвертое и пятое уравнения – система, из которой определяются динамические реакции  , и из нее же, разумеется, можно найти условия, при которых они равны нулю:
, и из нее же, разумеется, можно найти условия, при которых они равны нулю:
 ;
; 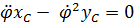 ;
;
 ;
; 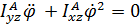 .
.
Так как движение произвольное, то выполнение этих равенств возможно только когда 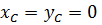 – статическая уравновешенность и
– статическая уравновешенность и 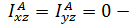 динамическая уравновешенность, т. е. динамические реакции равны нулю, если ось вращения является главной центральной.
динамическая уравновешенность, т. е. динамические реакции равны нулю, если ось вращения является главной центральной.
Рассмотрим пример. Ось вращения составляет с перпендикуляром к плоскости диска угол  (рис. 5.15,б). Диск статически уравновешен, т.е. центр масс лежит на оси вращения:
(рис. 5.15,б). Диск статически уравновешен, т.е. центр масс лежит на оси вращения: 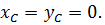 Масса диска
Масса диска  , радиус
, радиус  , диск совершает 12 000
, диск совершает 12 000  , расстояние между подшипниками
, расстояние между подшипниками  .
.
Первые два уравнения системы (5.37) дают  , а из четвертого и пятого находим
, а из четвертого и пятого находим 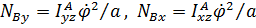 .
.
Центробежные моменты инерции найдем из теоремы Гюйгенса – Штейнера: 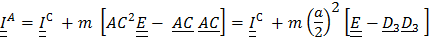 , где
, где
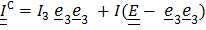 ,
, 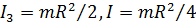 ;
;
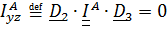 ,
, 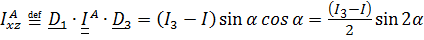 .
.
Таким образом,  ,
, 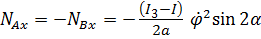 .
.
Для данных условий задачи и весьма незначительного угла 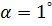 получим
получим 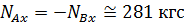 , что значительно превышает статическую реакцию 5 кгс.
, что значительно превышает статическую реакцию 5 кгс.
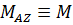 (рис. 5.15а).
(рис. 5.15а).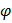
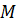
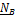
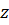
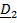
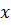 y
y 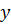 y
y 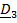
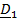
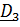
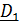
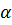
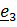
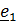
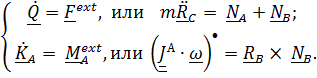 (5.36)
(5.36) , связанные с телом:
, связанные с телом: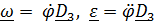 ,
, 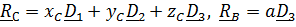 ;
; ;
;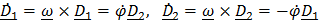 ;
;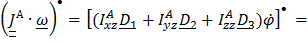
 ;
;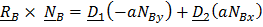 ;
;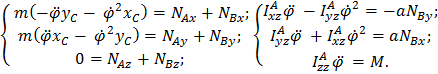 (5.37)
(5.37) , и из нее же, разумеется, можно найти условия, при которых они равны нулю:
, и из нее же, разумеется, можно найти условия, при которых они равны нулю: ;
; 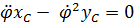 ;
; ;
; 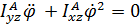 .
. – статическая уравновешенность и
– статическая уравновешенность и 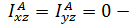 динамическая уравновешенность, т. е. динамические реакции равны нулю, если ось вращения является главной центральной.
динамическая уравновешенность, т. е. динамические реакции равны нулю, если ось вращения является главной центральной. (рис. 5.15,б). Диск статически уравновешен, т.е. центр масс лежит на оси вращения:
(рис. 5.15,б). Диск статически уравновешен, т.е. центр масс лежит на оси вращения: 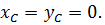 Масса диска
Масса диска  , радиус
, радиус  , диск совершает 12 000
, диск совершает 12 000  , расстояние между подшипниками
, расстояние между подшипниками  .
. , а из четвертого и пятого находим
, а из четвертого и пятого находим 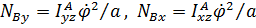 .
.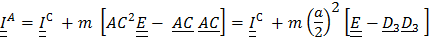 , где
, где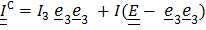 ,
, 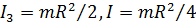 ;
;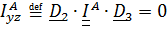 ,
, 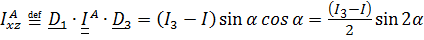 .
. ,
, 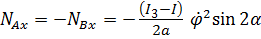 .
.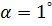 получим
получим 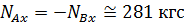 , что значительно превышает статическую реакцию 5 кгс.
, что значительно превышает статическую реакцию 5 кгс. 2015-02-04
2015-02-04 1644
1644
