Твердого тела. Теорема Кенига

Кинетическая энергия материальной точки: ;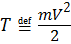

тела, состоящего из материальных точек:

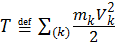; (5.38)

континуального тела:

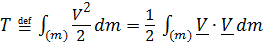. (5.39)

Для твердого тела 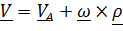. Подставим это выражение в (5.39):

.

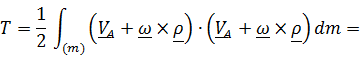
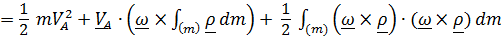Второе слагаемое равно 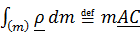, а подынтегральное выражение в третьем слагаемом преобразуем, чтобы вынести из интеграла постоянный вектор :

.

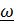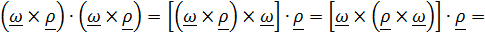
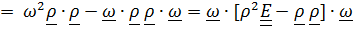Получим:

.

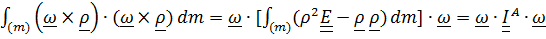Таким образом,

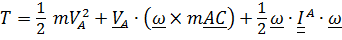. (5.40)

Рассмотрим частные случаи.

а) Тело вращается вокруг неподвижной точки :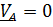

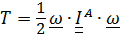. (5.41)

б) В качестве полюса взят центр масс :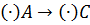

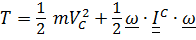. (5.42)

Формула (5.42) представляет собой частный случай (для твердого тела) теоремы Кенига:

Кинетическая энергия складывается из кинетической энергии поступательного движения со скоростью центра масс и энергии относительного движения относительно системы отсчета, движущейся поступательно со скоростью центра масс (для твердого тела относительное движение – вращение вокруг центра масс).

Для плоского движения 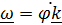и формулы (5.41), (5.42) примут вид:

вращение вокруг неподвижной оси – ;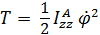

общий случай плоского движения – ,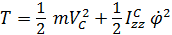

где осевые моменты инерции 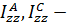постоянные величины.