Качение шара по внутренней поверхности вертикального цилиндра

Чтобы предотвратить проскальзывание, шарик массы 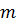и радиуса 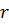катится с достаточно большой окружной скоростью (рис.5.14). Кажется правдоподобным, что траектория будет иметь вид спирали увеличивающейся крутизны.

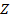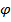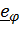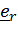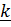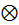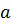Скорость и ускорение центра шарика в цилиндрической системе:

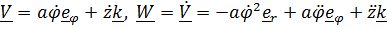. (1)

Уравнения движения:

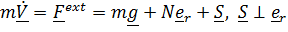, (2)

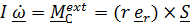, (3)

где 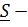составляющая реакции в касательной плоскости в точке касания.

Условие отсутствия проскальзывания

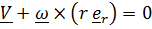, (4)

которое в координатной записи имеет вид 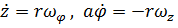, дополним его производной:

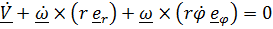. (5)

Выразим из (2) 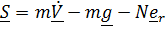, подставим его в (3) и найдем:

.

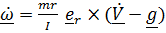Подставляя полученное выражение в (5), с учетом

,

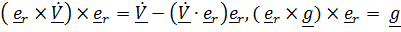получим:

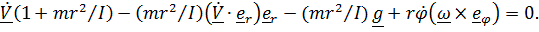(6)

Умножая скалярно уравнение (6) на 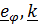, получим (проекция на 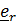равна нулю):

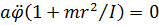, (7)

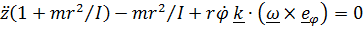. (8)

Из (7) следует 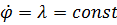, а в (8) величину 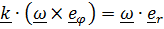найдем через ее же производную: 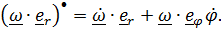Первое слагаемое в силу (3) равно нулю, а второе – с учетом (4) равно 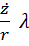, так что 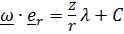(константу можно принять равной нулю). Окончательно получим:

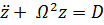, где обозначено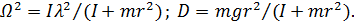

Решение этого уравнения имеет вид: 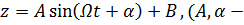постоянные, определяемые из начальных условий); оно показывает, что шарик совершает гармонические колебания по высоте (!). Игрокам в гольф и баскетболистам не так уж «не везет», когда шарик (мяч) выкатывается из лунки (из кольца).