Существует довольно узкий класс сил и моментов, мощность которых равна полной производной по времени от некоторой функции положения 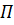 :
:
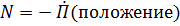 .
.
Такие воздействия называются потенциальными, а 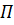 – потенциальной энергией (знак (–) принято ставить для удобства).
– потенциальной энергией (знак (–) принято ставить для удобства).
Если рассматривается мощность силы, то аргументом функции 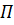 является вектор положения
является вектор положения 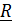 точки приложения силы, т. е.
точки приложения силы, т. е. 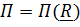 , а если мощность момента, то аргументом является тензор поворота, выраженный, например, через углы Эйлера, т. е.
, а если мощность момента, то аргументом является тензор поворота, выраженный, например, через углы Эйлера, т. е. 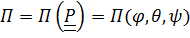 .
.
Для потенциальных сил и моментов элементарная работа является дифференциалом функции 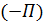 :
: 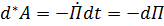 ; отсюда следует равносильное определение потенциальных воздействий: для них работа не зависит от пути перехода из первого положения во второе:
; отсюда следует равносильное определение потенциальных воздействий: для них работа не зависит от пути перехода из первого положения во второе:
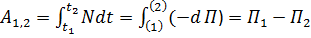 ;
;
и, как следствие, работа по замкнутому контуру равна нулю: 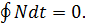
Если вектор силы известен, то условия его потенциальности можно получить, приравнивая элементарную работу дифференциалу энергии:
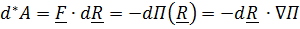 ,
,
где 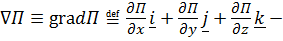 оператор Гамильтона (набла–оператор, градиент). Видно, что
оператор Гамильтона (набла–оператор, градиент). Видно, что 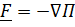 , т. е.
, т. е. 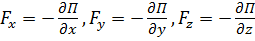 , и, поскольку смешанные производные не зависят от порядка дифференцирования, для потенциальной силы должны выполняться равенства:
, и, поскольку смешанные производные не зависят от порядка дифференцирования, для потенциальной силы должны выполняться равенства:
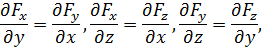
которые на языке дифференциальных операций векторного анализа равносильны равенству нулю ротора силы:
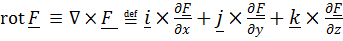 .
.
Примеры потенциальных воздействий
Однородное поле тяготения (рис. 5.16,a): 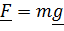 ,
, 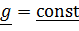 .
.
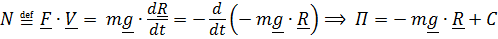 ,
,
или, если записать 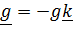 , то
, то 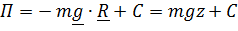 .
.
Энергия гравитации (рис. 5.16,б). Обозначим для краткости 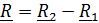 . Действующая на первое тело со стороны второго сила:
. Действующая на первое тело со стороны второго сила:
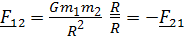 ; мощность
; мощность
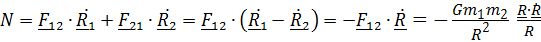 .
.
Дифференцируя равенство 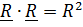 , получим
, получим 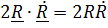 , поэтому
, поэтому
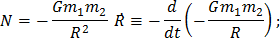
следовательно, 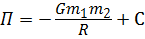 .
.
Принимая, что при бесконечном удалении тел 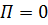 , получим
, получим 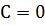 .
.
| Рис. 5.16. Потенциальные воздействия |
| a) |
| Z |
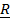 |
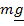 |
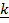 |
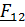 |
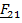 |
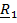 |
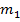 |
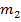 |
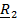 |
| б) |
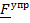 |
 |
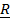 |
| в) |
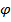 |
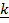 |
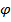 |
| г) |
Потенциальная энергия пружины.
а) Линейная пружина (Рис. 5.16,в):
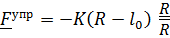 , где
, где 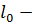 длина недеформированной пружины;
длина недеформированной пружины;
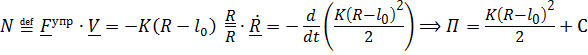 .
.
б) Спиральная пружина (Рис. 5.16,г):
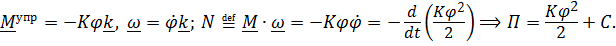
 2015-02-04
2015-02-04 730
730








