Мощность, рабо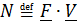та

Мощность силы , мощность момента .

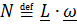Элементарная работа 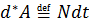. Символ 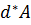означает, что элементарная работа не является в общем случае дифференциалом функции 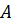ввиду произвольности сил и моментов. Для силы элементарная работа вычисляется по хорошо знакомой из курса физики формуле:

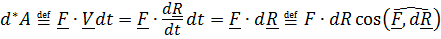, а вот для момента известная формула 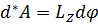имеет место только для плоского движения, когда 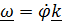, поэтому определение мощности как работы в единицу времени при произвольном движении тела становится весьма затруднительным.

Найдем мощность сил 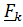и моментов 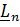, приложенных к твердому телу.

По определению 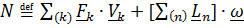. Подставив 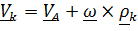и, переставив сомножители в смешанном произведении, получим:

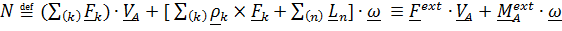. (5.43)

Ясно, что мощность (5.43) не зависит от выбора полюса А.