| Рис. 5.13. Качение по платформе |
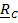 |
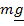 |
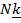 |
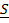 |
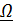 |
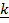 |
| • C |
| B |
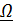 платформе катится шарик массы
платформе катится шарик массы 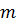 и радиуса
и радиуса 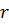 (рис. 5.13). Уравнения динамики (5.34) с учетом того, что тензор инерции – шаровой
(рис. 5.13). Уравнения динамики (5.34) с учетом того, что тензор инерции – шаровой 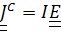 , принимают вид:
, принимают вид: 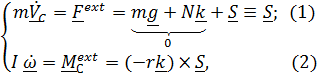
где 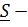 горизонтальная составляющая реакции платформы.
горизонтальная составляющая реакции платформы.
Добавим к (1),(2) условие отсутствия проскальзывания в точке касания В:
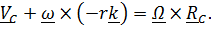 (3)
(3)
Исключим из уравнений все неизвестные, оставив только 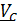 .Подставим
.Подставим 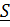 из первого уравнения во второе, умножим его векторно справа на
из первого уравнения во второе, умножим его векторно справа на 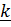 и, раскрывая двойное векторное произведение, получим:
и, раскрывая двойное векторное произведение, получим:
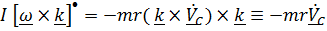 .
.
Подставив в это уравнение найденное из (3) выражение
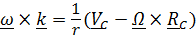 , получим
, получим 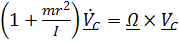 , или, обозначив
, или, обозначив 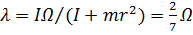 :
: 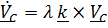 .
.
Подобное уравнение уже встречалось в (5.1.2), и решение его проще всего записать с помощью тензора поворота (напомним, 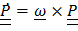 ):
):
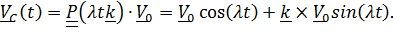
Таким образом, постоянный по величине вектор скорости «вращается» с постоянной угловой скоростью 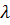 вокруг
вокруг 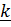 ; нетрудно понять, что это возможно, только если центр масс движется по окружности, радиус которой можно найти, проинтегрировав
; нетрудно понять, что это возможно, только если центр масс движется по окружности, радиус которой можно найти, проинтегрировав 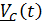 и подставив начальные условия:
и подставив начальные условия:
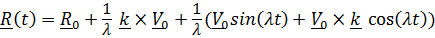 .
.
Таким образом, центр масс шарика движется по окружности радиуса  с центром в точке
с центром в точке 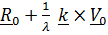 .
.
 2015-02-04
2015-02-04 739
739








