Все реальные тела ввиду их деформируемости обладают бесконечным числом степеней свободы, однако в качестве расчетной схемы можно выбрать систему с одной или несколькими степенями свободы. Так, например, плоское движение маятника может быть описано только углом поворота, если пренебречь его деформацией, а движение системы «диск – вал» также задается одним углом поворота, если пренебречь массой вала по сравнению с диском.
Наглядной моделью тела с одной степенью свободы, с помощью которой изучаются колебания, является грузик на пружине жесткости 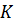 (рис. 7.1). На грузик действуют сила тяжести
(рис. 7.1). На грузик действуют сила тяжести 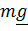 , сила упругости
, сила упругости 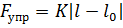 , возмущающая сила
, возмущающая сила  и пропорциональная скорости сила так называемого вязкого трения
и пропорциональная скорости сила так называемого вязкого трения 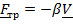 , которая моделируется демпфером.
, которая моделируется демпфером.
| Рис. 7.1. Тела с одной степенью свободы |
|
| x |
| mg |
| F |

|
| x |
Координату 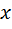 удобно отсчитывать из положения статического равновесия, в котором упругий элемент (пружина) уже имеет деформацию
удобно отсчитывать из положения статического равновесия, в котором упругий элемент (пружина) уже имеет деформацию 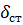 . Для безошибочного составления уравнений движения в качестве актуального следует взять состояние, при котором тело смещено в положительном направлении
. Для безошибочного составления уравнений движения в качестве актуального следует взять состояние, при котором тело смещено в положительном направлении 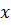 и имеет положительную же скорость
и имеет положительную же скорость  .
.
Запишем уравнение первого фундаментального закона (второго закона Ньютона) в проекции на ось 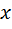 :
: 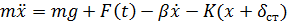 . В положении равновесия
. В положении равновесия 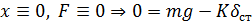 и уравнение принимает вид:
и уравнение принимает вид:
 .
.
Разделив на массу, получим каноническую запись уравнения:
 , (7.1)
, (7.1)
где обозначено 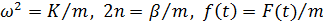 .
.
 2015-02-04
2015-02-04 321
321








