2015-02-04
425
По палубе раскачивающегося судна скользит материальная точка (рис. 6.4).
Ориентация палубы задается углами крена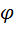 
и дифферента 
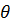.Тензор поворота 
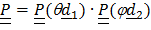переводит отсчетные 
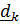в актуальные 
: 
.
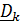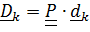Угловая скорость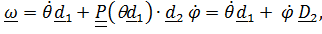 
положение точки 
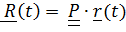, скорость 
, 
.
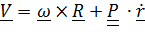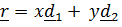Слагаемое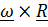 
– переносная скорость, 
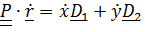– относительная.
Запишем все величины в актуальном базисе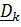 
:
;
;
;
;
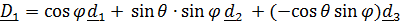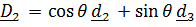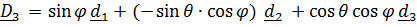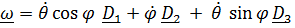| Рис. 6.4. Точка на качающейся поверхности |
|
|
|
|
|
|
|
|
.
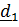
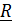
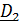
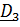
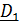
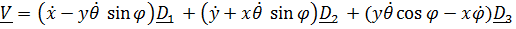Кинетическая энергия
;
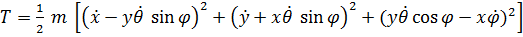мощность
+ 
+ 
+ 
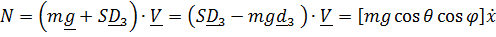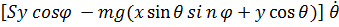где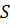 
– сила, с которой палуба действует на точку, а выражения в квадратных скобках – обобщенные силы.
Уравнения Лагранжа для координат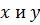 
имеют вид:
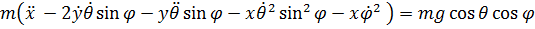; (1)
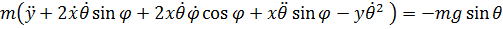. (2)
Уравнения для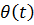 
и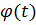 
имеют вид:
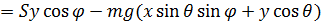; (3)
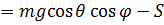. (4)
Уравнения (1), (2) и (4)– проекции уравнения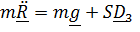 
на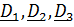 
, а уравнение (3) является их следствием – это проекция теоремы об изменении кинетического момента 
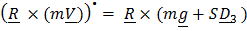на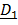 
. Задавая 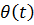и 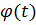, из (1) и (2) можно найти движение точки по палубе, а из уравнений для 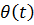(или 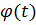) определим и реакцию 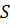. Строго говоря, постулирование 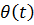и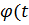 
) имеет физический смысл только при задании момента 
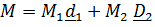, приложенного к даже лишенной массе палубе.
