2015-02-04
732
На тело действует гармоническая сила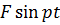 
с частотой 
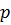и амплитудой 
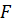. Уравнение (7.1) принимает вид:
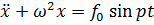. (7.3)
Общее решение неоднородного уравнения складывается, как известно, из решения однородного уравнения (7.2) и частного решения, т.е. любой функции, удовлетворяющей уравнению (7.3). В данном случае частное решение нетрудно угадать: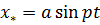 
. Подставляя его в (7.3), получим:
.
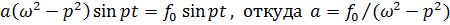Итак, общее решение
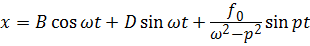. (7.3а)
Колебания с частотой вынуждающей силы называются чисто вынужденными колебаниями, поскольку при учете трения колебания с собственной частотой со временем затухают. В данном случае вынужденные колебания – частное решение:
.
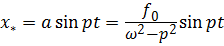Зависимость амплитуды вынужденных колебаний от частоты возмущающей силы (амплитудно– частотная характеристика (АЧХ)) представлена на рис. 7.2. При частоте возмущающей силы, равной собственной частоте, амплитуда колебаний стремится к бесконечности – это явление называют резонансом.
| Рис. 7.3.Резонанс |
| 2π |
 |
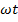| Рис. 7.2. АЧХ |
 |
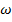| p |
 |
 |
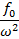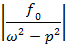Решение при резонансе получим как предел общего решения (7.3a) при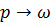 
, найдя предварительно из начальных условий значения постоянных:
,
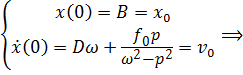
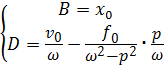и общее решение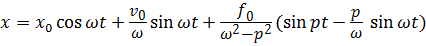 
.
Вычисляя при помощи правила Лопиталя предел при 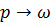, получим:
.
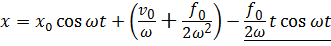Подчеркнутое слагаемое показывает рост размаха колебаний пропорционально времени (рис. 7.3).
