2015-02-04
1180
Дифференциальное уравнение имеет вид:
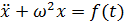(7.4)
Частное решение можно найти методом вариации произвольных постоянных: решение ищется в виде решения однородного уравнения, в котором коэффициенты являются неизвестными функциями времени:
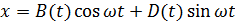. (7.4a)
Дифференцируя это выражение, получим:
.
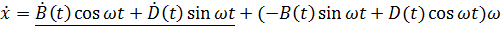Подчеркнутые слагаемые приравниваются нулю; это можно сделать, так как искомое частное решение представлено через две функции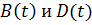 
.
Дифференцируя еще раз и подставляя результат в уравнение (7.4), получим: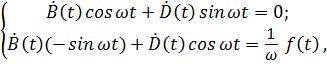 
откуда находим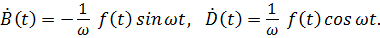 
Функции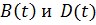 
можно записать в виде
.
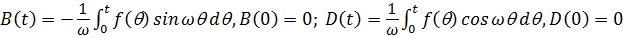Подставляя 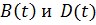в (7.4а) и внося 
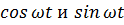в подинтегральное выражение, получим:
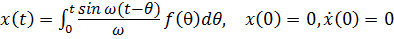. (7.5)
Интеграл (7.5) называется интегралом Дюамеля; его смысл выходит за рамки рассмотренной задачи. В интеграле (7.5)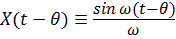 
– координата тела в актуальный момент времени 
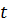при действии в момент 
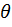единичного импульса, т.е. импульса, сообщающего системе единичную скорость. Действительно, решение уравнения 
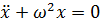при начальных условиях 
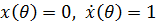имеет вид: 
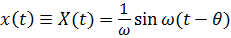. Поэтому (7.5) представляет собой суперпозицию движений линейной системы под действием элементарных импульсов силы 
.
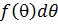В любой линейной задаче движение при произвольном воздействии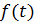 
и нулевых начальных условиях может быть найдено в виде
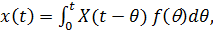
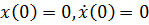, (7.6)
где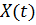 
– реакция системы на единичный импульс.
