Функция 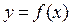 называется непрерывной в точке х 0, если:
называется непрерывной в точке х 0, если:
1) 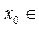 ООФ вместе с некоторой своей окрестностью;
ООФ вместе с некоторой своей окрестностью;
2) существует конечный предел 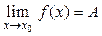 ;
;
3) этот предел совпадает со значением функции в точке х 0, т.е
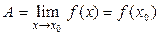 . (9)
. (9)
Все элементарные функции непрерывны в каждой точке своей области определения.
Если функция не является непрерывной в точке х 0, но она определена в окрестности этой точки (за исключением, быть может, самой точки х 0), то х 0 называется точкой разрыва функции.
Для определения вида разрыва в точке х 0 находят односторонние пределы 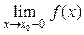 и
и 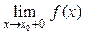 . При этом
. При этом
если существуют односторонние пределы 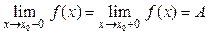 , но
, но 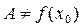 , то говорят, что функция терпит в точке х 0 разрыв типа выколотой точки;
, то говорят, что функция терпит в точке х 0 разрыв типа выколотой точки;
если существуют односторонние пределы 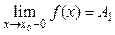 и
и
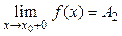 , но
, но 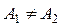 , то
, то 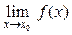 не существует; в этом случае говорят,
не существует; в этом случае говорят,
что функция терпит в точке х 0 разрыв типа«скачок»;
если левосторонний либо правосторонний (или оба) пределы функции
при 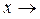 х 0 бесконечные, то говорят, что функция терпит в точке х 0 бесконечный разрыв.
х 0 бесконечные, то говорят, что функция терпит в точке х 0 бесконечный разрыв.
Разрывы типа выколотой точки и типа «скачок» относятся к конечным разрывам, или разрывам I рода, бесконечные разрывы относятся к разрывам II рода.
Примеры.
1) Функция 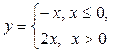 непрерывна
непрерывна 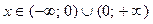 в силу непрерывности функций y = – х и y = 2 х. В точке х = 0 функция также непрерывна, т.к.
в силу непрерывности функций y = – х и y = 2 х. В точке х = 0 функция также непрерывна, т.к.
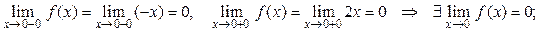
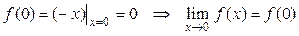 .
.
Следовательно, функция непрерывна для всех 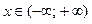 (рис. 9).
(рис. 9).
2) Функция 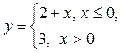 непрерывна
непрерывна 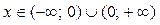 в силу непрерывности функций y = 2 + х и y = 3. В точке х = 0 функция терпит разрыв типа«скачок» (рис. 10), т.к.
в силу непрерывности функций y = 2 + х и y = 3. В точке х = 0 функция терпит разрыв типа«скачок» (рис. 10), т.к. 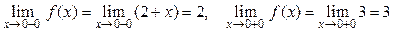 , следовательно,
, следовательно, 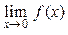 не существует.
не существует.
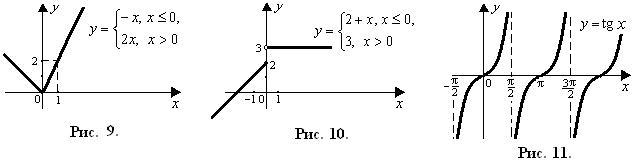
3) Функция y = tg x непрерывна во всех точках своей ООФ, т.е. для 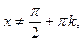
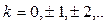 . В точках
. В точках 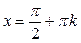 функция терпит разрывы II рода (рис. 11), т.к.
функция терпит разрывы II рода (рис. 11), т.к. 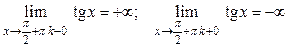 .
.
 2015-02-04
2015-02-04 428
428








