П.5. Вычисление пределов

При вычислении пределов используют теоремы о конечных пределах и теоремы обесконечно малых и бесконечно больших функциях.

Основные теоремы о конечных пределах.

1. Если f (x) = const (const – константа) при 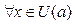, то

.

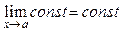2. 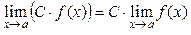, где C = const.

3. 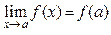, если f (x) – функция, непрерывная в точке х = а (см. п. 6).

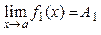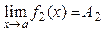4. Если и , где 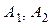– числа, то

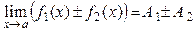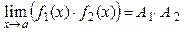, и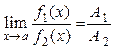

при условии, что .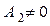

Теоремы обесконечно малых и бесконечно больших функциях

(для краткости обозначим: бм – бесконечно малая функция, бб – бесконечно большая функция, огр – локально ограниченная функция).

5. бм ± бм = бм.

6. бм × бм = бм.

7. бм × огр = бм.

8. 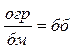, если огр не является бм.

9. бб + бб = бб, если обе бб одного знака.

10. бб × бб = бб.

11. бб × огр = бб, если огр не является бм.

12. .

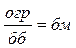Примеры.

1) 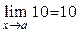(здесь использована теорема 1);

2) 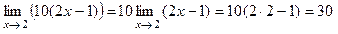(здесь использованы теоремы 2, 3 и непрерывность функции у = 2 х – 1);

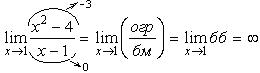
3) (здесь использована теорема 8);

4)

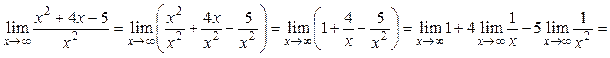
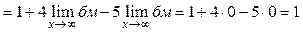(здесь использованы теоремы 2, 4 и 12).