П.1. Формула Ньютона–Лейбница

Формула Ньютона–Лейбницадля вычисления определенного интеграла имеет вид:

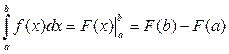, (7)

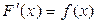если и 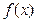непрерывна на .

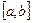Пример 4. Вычислить определенный интеграл .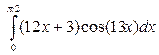

Решение. Это определенный интеграл, берущийся по частям, поэтому, применяя формулу (4), а затем формулу Ньютона – Лейбница, получаем:

= .

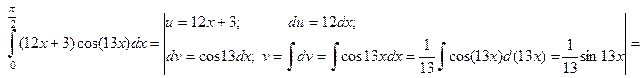
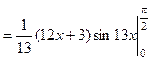
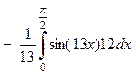
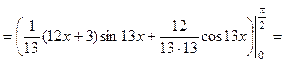
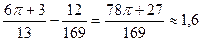Ответ: = .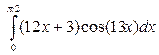

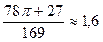п.2. Несобственные интегралы первого и второго рода

Примером несобственного интеграла первого рода является интеграл

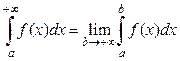(8)

Интегралы

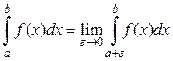, (9)

где a – точка бесконечного разрыва функци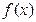и , и

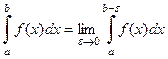, (10)

где b – точка бесконечного разрыва функции 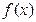, относятся к несобственным интегралам второго рода.

Несобственный интеграл называется сходящимся, если существует конечный предел в правой части равенства. Если же предел не существует или равен бесконечности, то интеграл называется расходящимся.

Пример 5. Исследовать на сходимость интеграл .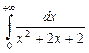

Решение. Это несобственный интеграл первого рода, поэтому

.

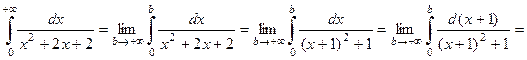
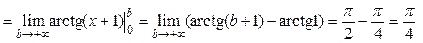Ответ: интеграл 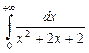сходится и равен .

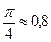Пример 6. Исследовать на сходимость интеграл .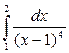

Решение. Это несобственный интеграл второго рода, так как х = 1 – точка разрыва второго рода подинтегральной функции, поэтому

,

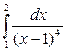
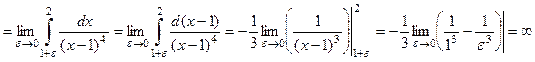следовательно, интеграл расходится.

Ответ: интеграл 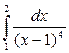расходится.

п.3. В ычисление площади плоской фигуры в декартовой системе