Дифференциальным уравнением называется уравнение вида
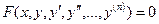 , (1)
, (1)
где х − независимая переменная, y=f(x) − искомая функция, 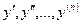 − ее производные.
− ее производные.
Решением дифференциального уравнения называется такая функция y=f(x), которая при подстановке ее и ее производных обращает равенство (1) в тождество.
Порядком дифференциального уравнения (1) называется наибольший порядок n входящей в него производной.
Интегрированием дифференциального уравнения называется процесс нахождения его решений.
Интегральной кривой называется график решения дифференциального уравнения.
Общим решением дифференциального уравнения (1) порядка n называется такое решение 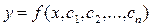 , которое является функцией от независимой переменной х и от n произвольных независимых постоянных
, которое является функцией от независимой переменной х и от n произвольных независимых постоянных 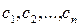 .
.
Частным решением называется решение, называется решение, получаемое из общего решения при некоторых конкретных значениях постоянных 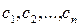 .
.
Пример:
Для уравнения второго порядка 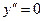 общее решение имеет вид
общее решение имеет вид 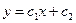 . Одним из частных решений будет решение у = х, полученное при
. Одним из частных решений будет решение у = х, полученное при 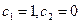 .
.
 2015-02-04
2015-02-04 240
240







