- Пусть X случайная величина, подчиненная биномиальному закону распределения. Тогда соответствующая ей последовательность вероятностей
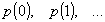 может иметь один из следующих трех видов:
может иметь один из следующих трех видов:
a) Нуль является наиболее вероятным значением X. Кроме нуля, наиболее вероятным значением может быть еще единица, так что 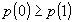 . Оставшиеся члены последовательности монотонно убывают. Наименее вероятным значением X является n.
. Оставшиеся члены последовательности монотонно убывают. Наименее вероятным значением X является n.
b) Наиболее вероятным значение X является n. Кроме n, наиболее вероятным значением может быть еще n-1. Оставшиеся члены последовательности монотонно возрастают от 0 до n-1. Наименее вероятным значением является нуль.
c) Члены последовательности возрастают и достигают максимума в одном или, возможно, в двух наиболее вероятных значениях X. После этого члены последовательности строго убывают. Наименее вероятными значениями X являются или нуль, или n, или они оба.
- Наиболее вероятное значение X, биномиальной случайной величины, равно наибольшему целому числу, не превосходящему произведения
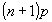 . Для существования двух наиболее вероятных значений X необходимо и достаточно, чтобы (n+1)p было целым числом. Тогда наиболее вероятными значениями X являются
. Для существования двух наиболее вероятных значений X необходимо и достаточно, чтобы (n+1)p было целым числом. Тогда наиболее вероятными значениями X являются 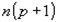 и
и 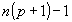 .
. - Если случайные величины
 независимы и имеют биномиальное распределение с параметрами
независимы и имеют биномиальное распределение с параметрами  и p, то сумма
и p, то сумма 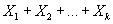 подчиняется биномиальному закону с параметрами
подчиняется биномиальному закону с параметрами 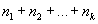 и p.
и p. - Сумма k независимых случайных величин b(m|ni,p)есть также биномиальная случайная величина b(m | n,p), у которой
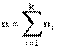
 2015-02-04
2015-02-04 695
695








