Биномиальное распределение (этот термин был впервые использован в работе Yule, 1911 г.) возникает в тех случаях, когда ставится вопрос: сколько раз происходит некоторое событие в серии из определенного числа независимых наблюдений (опытов), выполняемых в одинаковых условиях.
Биномиальное распределение возникло из наблюдений за простейшей азартной игрой Ч бросание правильной монеты. Во многих ситуациях эта модель служит хорошим первым приближением для более сложных игр и случайных процессов, возникающих при игре на бирже. Замечательно, что существенные черты многих сложных процессов можно понять, исходя из простой биномиальной модели.
Свое название она получила, от того, что значения P(m, n) являются членами в разложении (p + q) n по формуле бинома Ньютона:
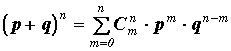
Поскольку p + q = 1, то
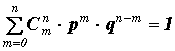
Эта формула просто иллюстрирует аксиому теории вероятностей, cогласно которой вероятность достоверного события равна единице.
Биномиальное распределение может обозначатся как: β(m | n,p).
Где: n — число испытаний. З -вероятность успеха (Схема Бернулли)
mÎ[0;n].
Дискретная случайная величина Х имеет биномиальное распределение, если она принимает значения 0,1,2,3,4..,n, с вероятностями:
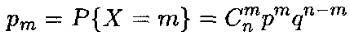
Случайная величина Х, распределенная по биномиальному закону, является числом успехов с вероятностью p в схеме Бернулли проведения n независимых опытов
Распределение дискретной случайной величины, имеющей биномиальное распределение, имеет вид:
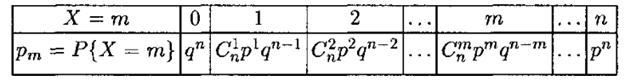
Контроль вероятности осуществляется по формуле:
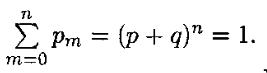
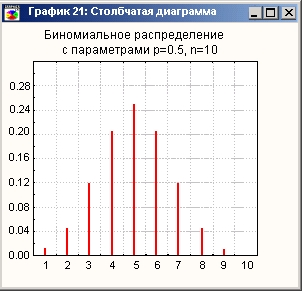
Гистограмма биномиального распределения
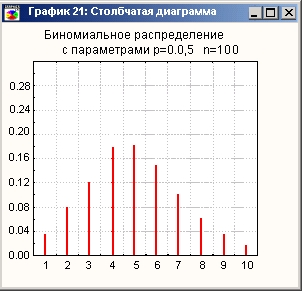
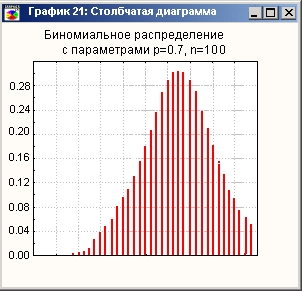
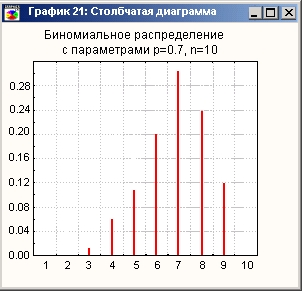
Числовые характеристики биномиального распределения
Функция распределения с.в. Х, распределенной по биномиальному закону,
Производящей функцией биномиального распределения является:
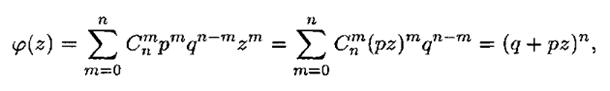 Возьмем первую и вторую производную от производящей функции, для нахождения числовых характеристик:
Возьмем первую и вторую производную от производящей функции, для нахождения числовых характеристик:
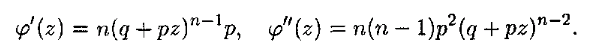
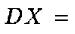
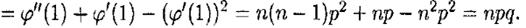


 2015-02-04
2015-02-04 2615
2615
