Уравнения Лагранжа 2-го рода: 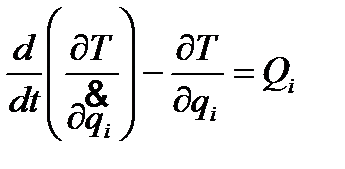 , (i=1,2…s) – дифференциальные уравнения второго порядка, s – число степеней свободы системы (число независимых координат); qi – обобщенная координата (перемещение, угол, площадь и др.);
, (i=1,2…s) – дифференциальные уравнения второго порядка, s – число степеней свободы системы (число независимых координат); qi – обобщенная координата (перемещение, угол, площадь и др.); 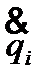 – обобщенная скорость (линейная скорость, угловая, секторная и др.),
– обобщенная скорость (линейная скорость, угловая, секторная и др.),
Т = Т(q1,q2,…,qS, 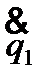 ,
, 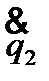 …
… 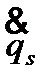 ,t) – кинетическая энергия системы,
,t) – кинетическая энергия системы,
Qi – обобщенная сила (сила, момент и др.), ее размерность зависит от размерности обобщенной координаты и размерности работы.
Для вычисления обобщенной силы, например Q1, задаем возможное перемещение, при котором все вариации обобщенных координат, кроме dq1, равны нулю:
dq1¹0, dq2= dq3=…= dqS= 0. Вычисляем на этом перемещении возможную работу dА1 всех активных сил, приложенных к системе. Имея dА1= Q1dq1, находим 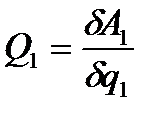 .
.
 2015-02-04
2015-02-04 546
546







