Доказательство

Пусть a – целое большее 1. Обозначив 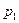, его наименьший делитель имеем

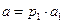. (1)

Если 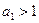, то обозначив 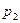его наименьший простой делитель,

имеем

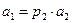. (2)

Если 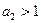, то аналогично получим

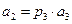. (3)

и так далее, пока не придем к какому-либо 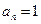. Тогда получим

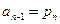. (n)

Перемножив (1), (2), (3),…,(n) и проведя сокращение получим следующее разложение на сомножители

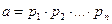. (A)

Допустим, что для a существует другое разложение

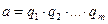. (Б)

Тогда

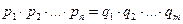. (В)

Правая часть равенства (В) делится на 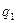. Следовательно, по крайней мере, один из сомножителей левой части делится на 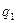. Пусть, например 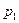делится на 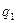(порядок следования сомножителей не играет роли). Тогда 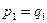( 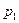кроме 1 делится только на 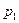). Сократив обе части равенства (В) на 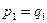, получим

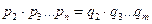. (Г)

Применив преждние рассуждения к (Г), получим

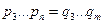. (Д)

и так далее пока, наконец, в одной части равенства, например, в левой не сократятся все сомножители. Но одновременно должны сократиться все сомножители левой части, так как равенство 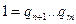при 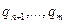превосходящих 1, невозможно.

Таким образом, второе разложение на простые сомножители тождественно первому.