λ=[λ]+{λ} |∙2;
2λ-2[λ]=2{λ}. Так как [2λ] ≤2λ, то
[2λ]-2[λ] ≤2{λ}<2;
[2λ]-2[λ] < 2. Отсюда [2λ]-2[λ]≤1. Что и требовалось доказать.
Обозначения. Пусть мы имеем n! и пусть 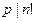 ,
, 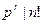 , но
, но 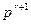 не делит n!, то говорят, что p входит в степени r в n!.
не делит n!, то говорят, что p входит в степени r в n!.
Теорема.
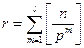 , где l – наибольшее такое, что
, где l – наибольшее такое, что 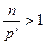 .
.
 2015-02-04
2015-02-04 267
267








