Определение. Главным моментом системы сил относительно полюса 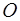 называется геометрическая сумма моментов всех сил системы относительно этого полюса.
называется геометрическая сумма моментов всех сил системы относительно этого полюса.
Обозначение: 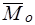 , или
, или 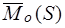 . Если задана система сил
. Если задана система сил 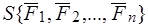 , то
, то
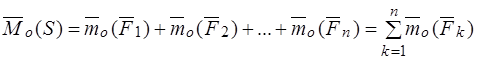 .
.
Определение. Главным моментом системы сил относительно оси 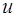 называется алгебраическая сумма моментов всех сил системы относительно этой оси.
называется алгебраическая сумма моментов всех сил системы относительно этой оси.
Обозначение: 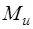 , или
, или 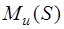
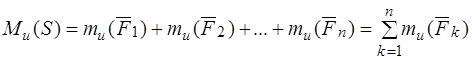 .
.
Теорема. Проекция главного момента системы сил относительно полюса 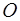 на ось
на ось 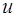 , проходящую через этот полюс, равна главному моменту сил системы относительно этой оси, то есть
, проходящую через этот полюс, равна главному моменту сил системы относительно этой оси, то есть
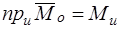 .
.
Доказательство:
Главный момент системы сил 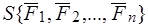 относительно полюса
относительно полюса 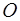
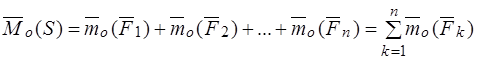 .
.
Спроектируем это векторное равенство на ось 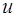 , проходящую через полюс
, проходящую через полюс 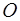 :
:
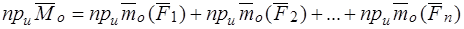 .
.
На основании теоремы о связи между моментом силы относительно полюса и моментом силы относительно оси
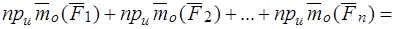
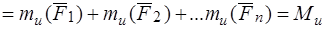 .
.
Следовательно 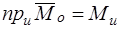 .
.
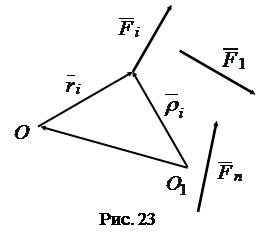 4.6. Зависимость между главными моментами системы сил относительно двух полюсов
4.6. Зависимость между главными моментами системы сил относительно двух полюсов
Дана система сил 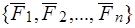 и два полюса: старый
и два полюса: старый 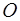 и новый
и новый 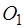 (рис. 23).
(рис. 23).
Главный момент системы сил относительно старого полюса:
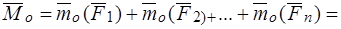
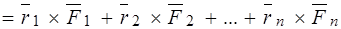 .
.
Главный момент относительно нового полюса:
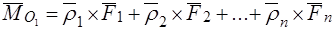 .
.
Здесь 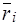 и
и 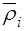 (
(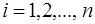 )–радиус-векторы точки приложения силы
)–радиус-векторы точки приложения силы 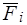 относительно старого и нового полюсов соответственно.
относительно старого и нового полюсов соответственно.
Из рисунка видно, что:
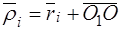
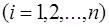 .
.
Тогда
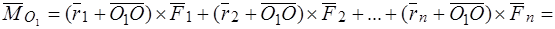
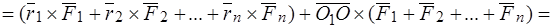
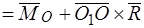 ,
,
где 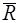 –главный вектор. Пришли к теореме о зависимости между главными моментами системы сил относительно двух полюсов.
–главный вектор. Пришли к теореме о зависимости между главными моментами системы сил относительно двух полюсов.
Теорема. Главный момент системы сил относительно нового полюса равен сумме главного момента системы сил относительно старого полюса и момента главного вектора, приложенного к старому полюсу относительно нового –полюса, то есть
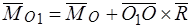 .
.
Следствие 1. Если главный вектор системы сил равен нулю, то ее главный момент не зависит от выбора полюса, то есть, если 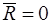 , то
, то 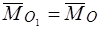 .
.
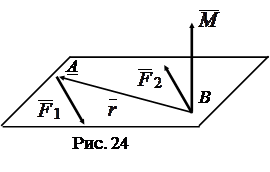 Следствие 2. Главный момент пары сил не зависит от выбора полюса и отличен от нуля.
Следствие 2. Главный момент пары сил не зависит от выбора полюса и отличен от нуля.
Дана пара сил {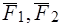 } (рис. 24).
} (рис. 24). 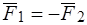 ,
, 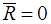 . Так как главный вектор
. Так как главный вектор 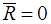 . То главный момент пары не зависит от выбора полюса:
. То главный момент пары не зависит от выбора полюса:
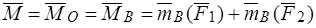 .
.
Линия действия силы 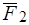 проходит через полюс
проходит через полюс 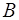 , то есть
, то есть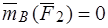 , и:
, и:
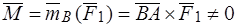 .
.
 2014-01-25
2014-01-25 1550
1550
