Будем предполагать для простоты, что частицы к-фазы представляют собой неизменяемые твердые сферы, одинакового диаметра. Такие среды принято называть монодисперсными, а в случае если диаметр у частиц разный – полидисперсными. В основу, как и ранее, положим законы сохранения массы, импульса и энергии. Запишем их для Лагранжевого объема связанного с газом.
Закон сохранения массы для смеси в целом:
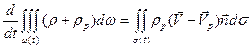 . (6.8)
. (6.8)
Закон сохранения импульса для смеси в целом:
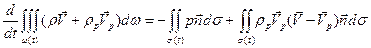 . (6.9)
. (6.9)
Закон сохранения энергии для смеси в целом:
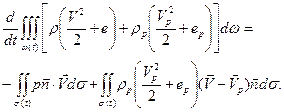 (6.10)
(6.10)
Члены, стоящие в левой части соотношений, представляют собой потоки массы, импульса и полной энергии “газа” частиц через границу s(t) подвижного объема w(t). Воспользуемся формулой дифференцирования по подвижному объему (2.7) и перейдем к Эйлерову объему
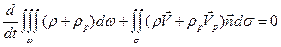 . (6.11)
. (6.11)
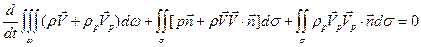 . (6.12)
. (6.12)
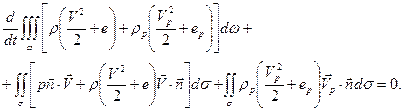 (6.13)
(6.13)
Так как обмен массой между фазами отсутствует, законы сохранения для газа и “газа” частиц примут вид:
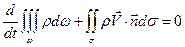 , (6.14)
, (6.14)
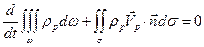 . (6.15)
. (6.15)
Динамическое взаимодействие фаз – обмен импульсом меду фазами (частицы могут тормозится или ускорятся газом, и наоборот) можно трактовать как воздействие на газ объемной силы fp пропорциональной плотности “газа” частиц rp. Запишем уравнение движения отдельной частицы
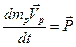 .
.
После несложных преобразований с учетом (6.2) оно примет вид:
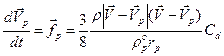 . (6.16)
. (6.16)
Получим так же уравнение теплообмена частицы с газом, в предположении справедливости закона теплообмена Ньютона, отсутствия теплообмена излучением, постоянства температуры частицы по ее радиусу:
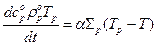 ,
,
или преобразуя с учетом (6.7)
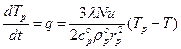 . (6.17)
. (6.17)
Тогда законы сохранения импульса для газа и “газа” частиц могут быть записаны в виде:
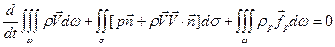 . (6.18)
. (6.18)
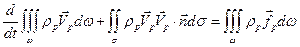 . (6.19)
. (6.19)
Легко видеть, что суммирование полученных уравнений дает закон сохранения импульса для всей смеси (6.12). Аналогично получим законы сохранения энергии для газа и “газа” частиц
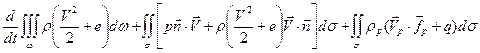 , (6.20)
, (6.20)
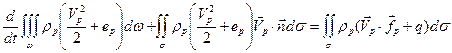 . (6.21)
. (6.21)
Таким образом, мы имеем две системы интегральных соотношений, связанных между собой источниковыми членами. Причем в соотношениях для “газа” частиц отсутствует “давление частиц”, так как в принятой модели динамический и энергетический обмен между частицами осуществляется только через газ. В последние десятилетия предлагаются такие модели. Введение “давления частиц” позволяет описать эффект динамического взаимодействия частиц между собой, который проявляется в областях с повышенной концентрацией к-фазы. В частности в так называемых пеленах – течениях типа струй из частиц, которые возникают за обтекаемыми двухфазным потоком твердыми поверхностями. Отсутствие в модели собственного “давления частиц”, в случае непрерывности параметров позволяет записать для “газа” частиц отдельно уравнения сохранения кинетической и внутренней энергии. Воспользуемся формулой Гаусса-Остроградского и учитывая произвольность w получим из (6.19)
 ,
,
умножим его скалярно на 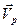
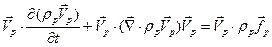 .
.
Используя очевидное равенство
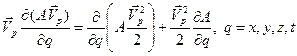 ,
,
выведем уравнение сохранения кинетической энергии для “газа” частиц:
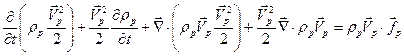 (6.22)
(6.22)
Интегрируя (6.22) по w и используя формулу Гаусса-Остроградского получим интегральный закон сохранения кинетической энергии для “газа” частиц:
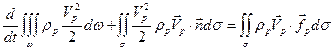 . (6.23)
. (6.23)
Вычитая его из (6.21) получаем закон сохранения тепловой энергии для “газа” частиц:
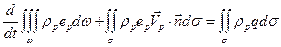 . (6.24)
. (6.24)
Напомним, что последние два соотношения справедливы для течений без разрывов. Для того, что бы распространить их на течения с разрывами необходимо дополнить их соотношениями об обмене кинетической и тепловой энергией при переходе через скачок. Если такого обмена нет, то (6.23), (6.24) справедливы и для разрывных течений. Аналогично можно получить дифференциальные соотношения и для остальных законов сохранения:
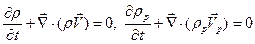 , (6.25)
, (6.25)
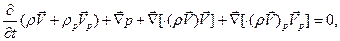 (6.26)
(6.26)
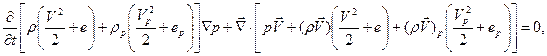 (6.27)
(6.27)
Уравнение движения частицы и теплообмена ее с окружающей средой
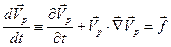 , (6.28)
, (6.28)
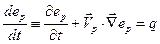 . (6.29)
. (6.29)
Используя re = rh – p из (6.26-29) получаем:
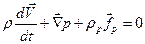 , (6.30)
, (6.30)
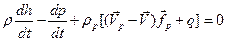 . (6.31)
. (6.31)
 2015-02-04
2015-02-04 588
588








