Равновесное и замороженное двухфазные течения

Рассмотрим одномерное приближение для случая установившегося непрерывного движения монодисперсной смеси и исследуем ряд предельных случаев такого движения. Полагая 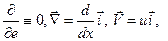после ряда простых преобразований, получим следующую систему обыкновенных дифференциальных уравнений:

Уравнение движения для частицы:

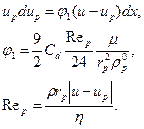(4.38)

Уравнение теплообмена между газом и частицей:

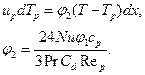(4.39)

Уравнение движения для смеси и частиц:

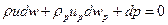. (4.40)

Уравнение сохранения энергии для смеси газа и частиц:

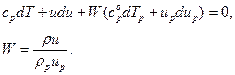(4.41)

Дополним систему уравнением состояния

.

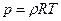Вводя число Маха для газа, получим из (4.40), (4.41) следующие уравнения справедливые для течения в канале переменного сечения:

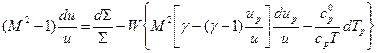, (4.42)

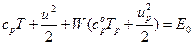. (4.43)

Рассмотрим уравнение (6.42). Пусть рассматриваемое нами течение газа ускоряющееся du > 0, тогда газ будет разгонять частицы Þ du_p > 0 и g > (g-1)u_p/u. Как известно dT < 0, и газ будет охлаждать частицы Þ dT_p < 0. Видно, что выражение в фигурных скобках {}>0. Таким образом, скорость звука для газа при двухфазном установившемся течении достигается в расширяющейся части сопла dL/L. Причем чем больше концентрация частиц в потоке W, тем дальше.

Рассмотрим предельный случай: j₁ ® ¥. Это случай очень мелких, легких частиц, динамическое и энергетическое взаимодействие которых с газом очень велико. При этом u» u_p, T» T_p, а рассматриваемое движение называется равновесным. Система уравнений описывающая такое течение имеет вид:

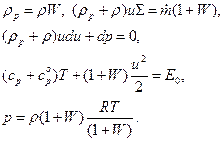(6.44)

Если ввести равновесные расход 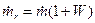, плотность 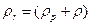, удельную теплоемкость 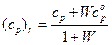, газовую постоянную 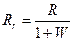, скорость 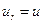, температуру 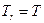, давление 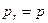и определить показатель адиабаты соотношением:

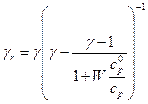, (6.45)

то уравнения для равновесных потоков в точности совпадут с уравнениями обычной газовой динамики. Таким образом, все закономерности для изоэнтропических течений, могут быть перенесены на равновесные двухфазные течения. Отметим, что подобные свойства имеют место и для течений с постоянными скоростным и температурным отставаниями частиц.

“ Равновесная ” скорость звука

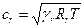, (6.46)

достигается в минимальном сечении сопла Лаваля. Из формулы (6.46) видно, что 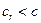. Очевидно, что можно определить “равновесное” число Маха

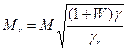. (6.47)

Второй предельный случай: j₁ ® 0, j₁ ® 0. Очевидно, что скорость и температура частиц остаются при этом неизменными. Обычно такое движение называют замороженным. Данное приближение часто используется для оценки максимальных динамического 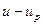и температурного .

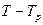Приложение 1. Краткие сведения из математики.

В данном разделе приводятся без доказательств основные математические соотношения, используемые в МСС.

Скаляр – это величина, значением которой является вещественное число.

Функция f (x) – отображает числовой аргумент x в числовое значение функции y = f (x). Функцию представляют в виде графиков и таблиц (в одной колонке аргумент, в другой – значение функции). Наряду с функцией одной переменной, рассматривают функции нескольких переменных 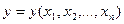. Например, уравнение состояния газа задает давление как функцию плотности и температуры: p = F (ρ, T). Функцию двух переменных удобно изображать графически в виде карты изолиний (линий уровня) функции.

В случае одной или нескольких переменных можно говорить о совокупности значений скалярной функции, которое называется скалярным полем этой функции (поле температур, поле давления).

Вектор 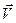- это объект, который характеризуется абсолютной величиной 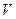и ориентацией в пространстве (направлением). Сам вектор не зависит от системы координат, однако в каждой заданной системе координат, можно определить проекции вектора на три координатные оси, и это будут компоненты вектора в данной системе координат. В прямоугольной декартовой системе координат компоненты вектора 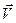, 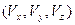- это скалярные функции, которые однозначно задают вектор.

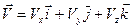
а его модуль (длина) 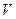вычисляется по формуле

.

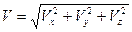Поле векторной величины – распределение вектора над областью изменения аргумента. Для определения векторного поля 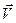достаточно задать систему координат и скалярные поля компонент вектора.