Задача 1.1. На первом блюде лежат 8 апельсинов, на втором – 4 яблока. Сколькими способами можно выбрать один фрукт?
Решение. Один апельсин можно выбрать восемью способами, а одно яблоко – четырьмя. Один фрукт – это либо апельсин, либо яблоко. Воспользуемся правилом суммы: m = 8, n = 4; число способов выбора одного фрукта m + n = 12.
Ответ: 12.
Задача 1.2. Сколько трёхзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 9, если:
а) число записано разными цифрами?
б) цифры в записи числа могут повторяться?
Решение. а) Первую цифру в записи числа можно выбрать шестью способами (ноль не может быть первой цифрой), для выбора второй цифры, отличающейся от первой, существует 6 способов (ноль может быть второй цифрой), а для выбора третьей цифры остаётся 5 способов (две цифры из имеющихся семи поставлены на первое и второе места). Таким образом, согласно правилу произведения получаем 6 · 6 · 5 = 180 способов составления трёхзначного числа, записанного разными цифрами.
б) Если цифры в записи числа могут повторяться, то имеем 6 способов выбора первой цифры и по 7 способов выбора каждой из следующих цифр. Количество таких чисел 6 · 7 · 7 = 294.
Ответ: а) 180; б) 294.
Задача 1.3. Студенты изучают 6 различных дисциплин. Если ежедневно в расписание включается по 3 различных дисциплины, то сколькими способами могут быть распределены занятия в день?
Решение. Различные комбинации трёх дисциплин, выбранных из шести, составляют расписание на один день. При этом они различаются либо составом дисциплин, либо их порядком. Поэтому искомое число определяется формулой числа размещений: 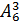 = 6·5·4 = 120.
= 6·5·4 = 120.
Ответ: 120.
Задача 1.4. Сколько шестизначных чётных чисел можно составить из цифр 1, 3, 4, 5, 7, 9, если в каждом из этих чисел ни одна цифра не повторяется?
Решение. Чтобы число было чётным, последняя его цифра (число единиц) должна быть чётной. Из заданных цифр только одна чётная – это 4. Поэтому последней цифрой искомого числа может быть только 4. Остальные пять цифр могут стоять на первых пяти местах в любом порядке. Значит, задача сводится к нахождению числа перестановок из пяти элементов: 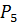 = 5!= 1·2·3·4·5 = 120.
= 5!= 1·2·3·4·5 = 120.
Ответ: 120.
Задача 1.5. Сколько шестизначных чётных чисел можно составить из цифр 1, 3, 4, 5, если цифры в записи числа могут повторяться?
Решение. Чтобы число было чётным, последняя его цифра (число единиц) должна быть чётной. Из заданных цифр только одна чётная – это 4. Поэтому последней цифрой искомого числа может быть только 4. Остальные пять цифр могут быть любыми из предложенных, причём могут повторяться. Значит, задача сводится к нахождению числа размещений с повторениями из четырёх элементов по пять в каждом: 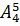 =
= 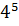 = 1024.
= 1024.
Ответ: 1024.
Задача 1.6. Сколькими способами можно выбрать 3 книги из 10 книг по математике, имеющихся в библиотеке?
Решение. Искомое число способов равно числу сочетаний из 10 элементов по 3 элемента в каждом, так как интересующие нас комбинации из трёх книг отличаются друг от друга только содержащимися в них книгами, а порядок расположения книг в этих комбинациях роли не играет. Следовательно, находим: 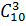 =
=  = 120.
= 120.
Ответ: 120.
Задача 1.7. Сколько трёхзначных чётных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры в записи числа могут повторяться?
Решение. При составлении трёхзначного числа из данных цифр в качестве первой цифры (числа сотен) можно взять любую цифру, кроме 0. Значит, есть шесть возможностей выбора первой цифры. В качестве второй цифры (числа десятков) можно выбрать любую из данных в условии цифр. Значит, есть семь возможностей выбора второй цифры. В качестве последней цифры (числа единиц) можно взять любую из цифр 0, 2, 4, 6. Значит, есть четыре возможности выбора третьей цифры. Следовательно, согласно правилу произведения находим количество способов составления числа, удовлетворяющего условию задачи: 6 · 7 · 4 = 168.
Ответ: 168.
Задача 1.8. Сколько различных чисел можно составить из цифр 4 и 5, если количество цифр в записи числа не более пяти и не менее трёх?
Решение. По условию задачи количество цифр в записи числа не более пяти и не менее трёх. Значит, их либо три, либо четыре, либо пять.
Если число, записанное четвёрками и пятёрками, содержит три цифры, то таких чисел будет: 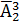 =
= 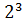 = 8.
= 8.
Если число, записанное четвёрками и пятёрками, содержит четыре цифры, то таких чисел будет: 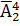 =
= 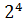 = 16.
= 16.
Если число, записанное четвёрками и пятёрками, содержит пять цифр, то таких чисел будет: 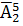 =
= 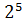 = 32.
= 32.
Следовательно, согласно правилу суммы, находим количество способов составления числа, удовлетворяющего условию задачи: 8 + 16 + 32 = 56.
Ответ: 56.
Задачи
1.1. Вычислите:
а) 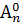 ; б)
; б) 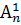 ; в)
; в) 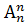 ; г)
; г) 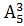 ; д)
; д) 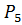 ; е)
; е) 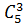 ; ж)
; ж) 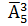 .
.
1.2. Вычислите:
а) 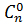 ; б)
; б) 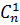 ; в)
; в) 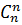 ; г)
; г)  ; д)
; д) 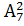 ; е)
; е) 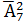 ; ж)
; ж) 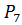 .
.
з) Докажите, что 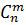 =
= 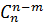 и вычислите
и вычислите 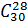 .
.
1.3. Комиссия состоит из председателя, его заместителя и ещё пяти человек. Сколькими способами члены комиссии могут распределить между собой обязанности?
1.4. В розыгрыше первенства по футболу принимают участие 18 команд. Сколькими способами могут распределиться золотая, серебряная и бронзовая медали, если любая команда может получить только одну медаль?
1.5. В группе из 10 человек надо выбрать трёх для уборки помещения. Сколько можно сделать различных вариантов такого выбора?
1.6. В студенческой группе 25 человек. Из них надо выбрать четверых для участия в студенческой конференции. Сколькими способами можно это сделать?
1.7. Сколькими способами можно расставить на одной книжной полке 7 книг разных авторов?
1.8. Сколькими способами можно рассадить компанию из шести человек за столом, накрытым шестью приборами?
1.9. Во взводе 3 сержанта и 30 солдат. Сколькими способами можно выделить одного сержанта и трёх солдат для патрулирования?
1.10. Хоккейная команда состоит из двух вратарей, семи защитников и десяти нападающих. Сколькими способами тренер может образовать стартовую шестёрку, состоящую из вратаря, двух защитников и трёх нападающих?
1.11. Обычно наибольшее количество очков на одной кости игры домино равно 12. Сколько костей содержала бы игра, если бы это число равнялось 18?
1.12. Сколько костей содержала бы игра домино, если бы наибольшее количество очков на одной кости равнялось 20?
1.13. Сколько различных десятизначных чисел можно написать, используя цифры 1 и 2?
1.14. Сколько различных восьмизначных чисел можно написать, используя цифры 0,1,2?
1.15. На пять сотрудников выделены три премии. Сколькими способами их можно распределить, если:
а) размер премий различен?
б) все премии одинаковые?
1.16. В классе 30 учащихся. Сколькими способами из них можно выделить двух человек для дежурства по школе, если:
а) один из них должен быть старшим?
б) старшего быть не должно?
1.17. Сколько диагоналей имеет выпуклый 12-угольник?
1.18. Сколько диагоналей имеет выпуклый 17-угольник?
1.19. Сколько существует двузначных чисел, записанных различными нечётными цифрами?
1.20. Сколько существует трёхзначных чисел, записанных различными нечётными цифрами?
1.21. Сколькими способами можно разложить пять различных писем по пяти различным конвертам, если в каждый конверт кладётся только одно письмо?
1.22. В розыгрыше первенства по футболу было сыграно 153 матча. Каждые две команды встречались между собой один раз. Сколько команд участвовало в розыгрыше первенства?
1.23. Из двух математиков и восьми экономистов надо составить комиссию из восьми человек. Сколькими способами может быть составлена комиссия, если в неё должен входить хотя бы один математик?
1.24. Из группы в 15 человек должны быть выделены бригадир и 4 члена бригады. Сколькими способами это можно сделать?
1.25. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
1.26. Буквы азбуки Морзе представляют собой набор точек и тире. Сколько букв может быть в азбуке Морзе, если буква не должна содержать более четырёх знаков?
1.27. Сколько различных двузначных чисел можно образовать из цифр 1,2,3,4, если:
а) в каждом числе цифры не повторяются?
б) цифры в числе могут повторяться?
1.28. Сейф запирается на замок, состоящий из пяти дисков, на каждом из которых изображены цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Замок открывается, если на дисках набрана определённая комбинация цифр. Хватит ли десяти дней на открытие сейфа, если "рабочий день" продолжается 13 часов, а на набор одной комбинации цифр уходит 5 секунд?
Ответы
1.1. а) 1; б) n; в) n!; г) 60; д) 120; е) 10; ж) 125;
1.2. а) 1; б) n; в) 1; г) 21; д) 42; е) 49; ж) 5040; з) 435;
1.3. 42;
1.4. 4896;
1.5. 120;
1.6. 12650;
1.7. 5040;
1.8. 720;
1.9. 12180;
1.10. 5040;
1.11. 55;
1.12. 66;
1.13. 1024;
1.14. 4374;
1.15. а) 60; б) 10.
1.16. а) 870; б) 435;
1.17. 54;
1.18. 119;
1.19. 20;
1.20. 60;
1.21. 120;
1.22. 18;
1.23. 44;
1.24. 15015;
1.25. 900;
1.26. 30;
1.27. а)12; б)16;
1.28. Может не хватить времени, так как всего возможных комбинаций 100000, а за 10 дней работы по 13 ч в день можно набрать только 93600 комбинаций.
 2015-02-04
2015-02-04 27971
27971








