Статистическое распределение выборки. Полигон и гистограмма

Определение 7. Статистической функцией распределения (или функцией распределения выборки) называется функция 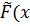), задающая для каждого значения 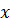статистического ряда относительную частоту события X < x,

т.е. ) ,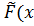

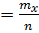где n – объем выборки; 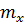– число выборочных значений, меньших x.

Свойства функции 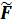(х)

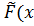1. 0 ≤ ) ≤1;

2. 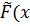) – неубывающая функция;

3. 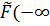) = 0, 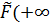)=1.

Замечание 2. В дальнейшем интегральную функцию распределения 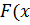) генеральной совокупности Х будем называть теоретической, а функцию 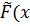) – эмпирической функцией распределения. Отличие между ними состоит в том, что 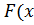) – вероятность события X < x, а 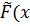) – его суммарная относительная частота в n опытах. Однако функци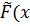и ) и 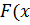) обладают одинаковыми свойствами.

Определение 8. Полигоном (или многоугольником) статистического распределения называется ломаная линия на плоскости Oxy, соединяющая точки (x_i ; m_i / n), i = 1, … k,

где n – объем выборки; x_i – значения статистического ряда; m_i ‒ число значений x_i в этом ряде (рис. 7.1).

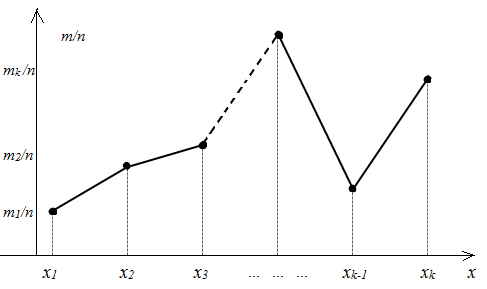
Рис. 7.1

Определение 9. Гистограммой интервального статистического ряда называется ступенчатая фигура, построенная по правилу: на плоскости Oxy на отрезках, изображающих интервалы статистического ряда, как на основаниях, строят прямоугольники с высотами, равными относительным частотам соответствующих интервалов (рис. 7.2).

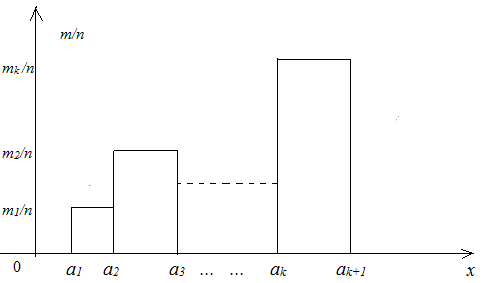
Рис. 7.2

Замечание 3. Полигон и гистограмма являются графическими приближениями дифференциальной функции распределения исследуемой случайной величины.