Исследование статистических различий между двумя выборками

Постановка задачи о проверке значимости различий.

Гипотеза однородности выборок

Пусть для изучения некоторой переменной C сформированы две выборки:

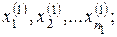
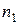– объем первой выборки;

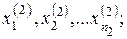
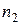– объем второй выборки.

Получение этих выборок может отличаться по времени регистрации, месту сбора информации, типу объектов и т.д.

Возникает вопрос: значимо либо незначимо различаются эти выборки? Другими словами, извлечены эти выборки из одной и той же генеральной совокупности либо их следует отнести к различным генеральным совокупностям?

Проведем данную описательную постановку вопроса на математический язык и сведем к задаче проверки статистической гипотезы.

Выдвинем нулевую гипотезу 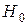, состоящую в том, что генеральные совокупности, из которых извлечены данные выборки, одинаковы, т.е. имеют одинаковые функции распределения:

,

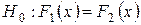при альтернативной гипотезе

.

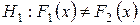Выдвинутая гипотеза означает отсутствие статистических различий и называется гипотезой однородности выборок. Таким образом, возникает следующая математическая задача:требуется на заданном уровне значимости 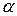проверить гипотезу однородности 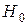об отсутствии статистических различий между двумя выборками.

Различным конкретизациям гипотезы однородности 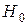соответствуют свои критерии проверки, которые называются критериями однородности.

Критерий однородности Фишера – Стьюдента

Этот объединенный критерий состоит в последовательном применении к данным выборкам классических критериев Фишера и Стьюдента.

Критерий Фишера

Условия применимости этого критерия:

· данные выборки независимые;

· соответствующие генеральные совокупности имеют нормальное распределение.

Поскольку нормальный закон распределения имеет два параметра 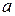и 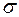, то для совпадения функций распределения 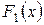и 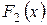достаточно убедиться в соответствующих равенствах одноименных параметров. Предварительно следует проверить гипотезу о равенстве генеральных дисперсий.

На заданном уровне значимости 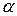для данных выборок (при указанных предположениях) проверяется гипотеза о равенстве генеральных дисперсий:

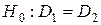при .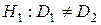

В качестве статистики критерия проверки используется случайная величина

,

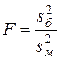характеризующая отношение большей "исправленной" дисперсии к меньшей. Установлено, что эта случайная величина F при условии справедливости выдвинутой гипотезы 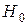имеет распределение Фишера с 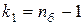и 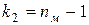степенями свободы. Здесь 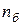– объем выборки, по которой вычислена большая "исправленная" дисперсия, а 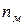– объем выборки с меньшей "исправленной" дисперсией.

По данным выборкам вычисляем наблюдаемое значение статистики Фишера .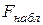

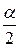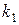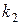По таблице квантилей распределения Фишера (табл.П7)[7] для уровня значимости (вдвое меньше заданного) и найденным числам степеней свободы и определяем критическую точку статистики Фишера в соответствии с равенством

,

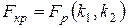где 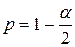(порядок квантили).

Критерий Фишера (разрешающее правило) проверки гипотезы однородности 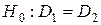состоит в следующем:

1. Если 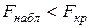, то гипотеза 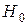сохраняется (генеральные дисперсии практически совпадают).

2. Если же 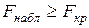, то гипотеза 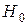решительно отвергается (выборки значимо отличаются друг от друга).

Критерий Стьюдента

Он применяется после критерия Фишера только в том случае, если гипотеза о равенстве генеральных дисперсий по критерию Фишера сохраняется.

Условия применимости критерия Стьюдента:

· выборки независимые;

· генеральные совокупности имеют нормальное распределение;

· независимые генеральные дисперсии равны .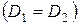

Заметим, что последнее требование при последовательном применении критериев будет автоматически выполнено.

На заданном уровне значимости 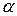для данных выборок проверяется гипотеза о равенстве генеральных математических ожиданий:

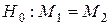при .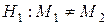

В качестве статистики критерия проверки используется случайная величина

.

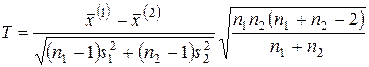Установлено, что при условии справедливости выдвинутой гипотезы 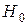эта случайная величина имеет t -распределение Стьюдента с 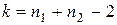степенями свободы.

По данным выборок вычисляем наблюдаемое значение статистики Стьюдента .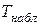

По таблице квантилей распределения Стьюдента (табл.П6)[8] для заданного уровня значимости 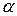и найденного числа степеней свободы 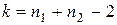определяем критическую точку статистики Стьюдента в соответствии с равенством

,

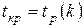где 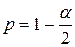(порядок квантили).

Разрешающее правило проверки гипотезы 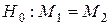состоит в следующем:

1 Если 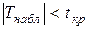, то гипотеза 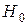сохраняется (генеральные математические ожидания практически совпадают).

2 Если же 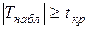, то гипотеза 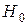отвергается (выборки значимо различаются друг от друга).

Примечание: При применении объединенного критерия Фишера – Стьюдента обязательным требованием является нормальность распределения. При этом гипотеза однородности (об отсутствии значимых статистических различий между выборками) подтверждается только в случае сохранения обеих гипотез, проверяемых соответственно по критерию Фишера (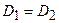) и критерию Стьюдента (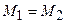). Если хотя бы одна из этих частных гипотез отвергается, то можно уверенно утверждать о наличии значимых статистических различий между данными выборками.

Критерий однородности Вилкоксона

Этот критерий рекомендуется применять в тех случаях, когда распределение генеральной совокупности отличается от нормального или это распределение фактически неизвестно.

Условия применимости критерия Вилкоксона:

· изучаемая переменная является непрерывной случайной величиной;

· данные выборки независимые;

· .

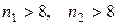На заданном уровне значимости 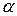проверяется гипотеза однородности (об отсутствии значимых статистических различий между данными выборками):

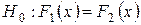при .

Пр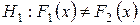едварительно расположим элементы обеих выборок в виде одного объединенного вариационного ряда (в порядке неубывания наблюдаемых значений). Каждому элементу объединенного ряда присвоим ранг – порядковый номер в ряде. Если несколько элементов объединенного ряда совпадают по величине, то применим так называемый способ средних рангов, а именно каждому из элементов однородной группы присвоим ранг, равный среднему арифметическому их порядковых номеров.

Пусть 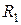– сумма рангов элементов 1-й выборки, 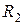– сумма рангов элементов 2-й выборки.

Составим выражения ,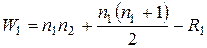

;

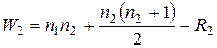при этом должно соблюдаться контрольное соотношение

.

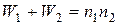Найдем величину .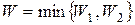

В качестве статистики критерия Вилкоксона проверки гипотезы однородности используется случайная величина

.

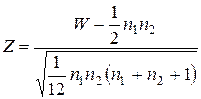Установлено, что при условии справедливости выдвинутой гипотезы 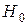эта случайная величина Z имеет стандартное нормальное распределение 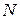(0;1).

По данным выборок вычисляем наблюдаемое значение статистики Вилкоксона .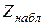

По таблице квантилей стандартного нормального распределения 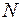(0;1) (табл.П1)[9] для заданного уровня значимости 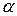определяем критическую точку статистики Z в соответствии с равенством:

,

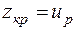где 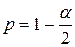(порядок квантили).

Разрешающее правило (критерий) проверки гипотезы однородности 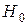заключается в следующем:

1. Если 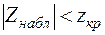, то гипотеза 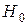сохраняется (выборки практически однородны).

2. Если же 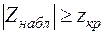, то гипотеза 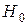решительно отвергается (выборки значимо отличаются друг от друга).

Пример. Даны две независимые выборки

–

–

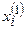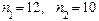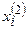Требуется на уровне значимости 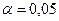проверить гипотезы однородности этих выборок с помощью:

1) критерия однородности Фишера – Стьюдента;

2) критерия Вилкоксона.

Решение поставленной задачи начнем с применения объединенного критерия Фишера – Стьюдента при молчаливом предположении нормальности распределения.

1. Сначала с помощью критерия Фишера проверим гипотезу о равенстве генеральных дисперси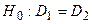й при .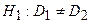

Предварительно для данных выборок найдем выборочные средние и исправленные дисперсии:

.

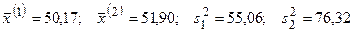Далее вычислим наблюдаемое значение статистики Фишера:

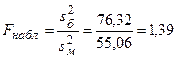
и найдем числа степеней свободы:

, .

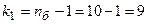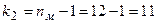По таблице квантилей распределения Фишера определим критическую точку статистики Фишера:

.

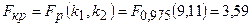Заметим, что порядок квантили .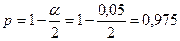

Сравнивая 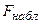и 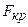, обнаруживаем, что 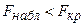, и в соответствии с разрешающим правилом критерия Фишера заключаем, что гипотеза о равенстве генеральных дисперсий сохраняется.

Теперь с помощью критерия Стьюдента проверим гипотезу о равенстве генеральных математических ожидани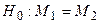й при .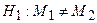

Для этого вычислим наблюдаемое значение статистики Стьюдента:

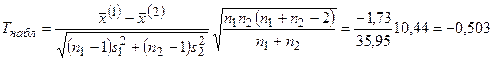
и найдем число степеней свободы .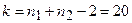

По таблице квантилей распределения Стьюдента определим критическую точку статистики Стьюдента:

.

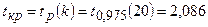Так как 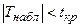, то в соответствии с разрешающим правилом критерия Стьюдента заключаем, что и гипотеза о равенстве математических ожиданий сохраняется.

Таким образом, согласно объединенному критерию Фишера – Стьюдента данные выборки практически однородны, т.е. различаются статистически незначимо.

2. Перейдем к применению критерия однородности Вилкоксона.

Сначала расположим элементы обеих выборок в виде одного объединенного вариационного ряда и присвоим им порядковые номера (условно строгая ранжировка). При этом элементы второй выборки для отчетливости их выделения пометим чертой сверху:

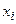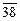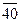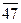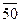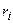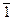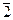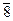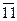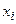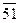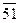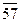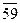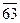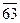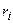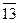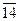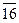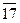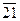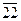Затем применим способ средних рангов:

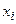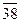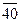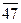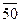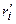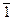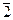				4,5	4,5	6,5	6,5		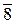	10,5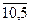
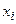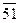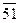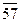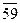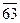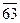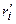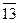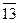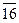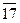							18,5	18,5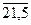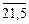

Далее последовательно находим

;

.

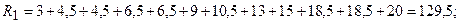
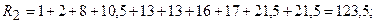
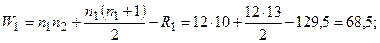
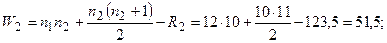
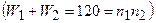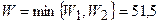Затем вычисляем наблюдаемое значение статистики Вилкоксона:

.

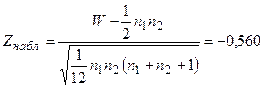По таблице квантилей стандартного нормального распределения 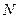(0;1) для заданного уровня значимости 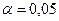определяем критическую точку статистики Z:

.

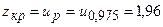Так как 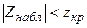, то в соответствии с разрешающим правилом критерия Вилкоксона заключаем, что гипотеза однородности 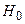сохраняется, что свидетельствует об отсутствии значимых статистических различий между двумя данными выборками.