| Рис. 15 Расчет интервальной оценки математического ожидания и дисперсии |
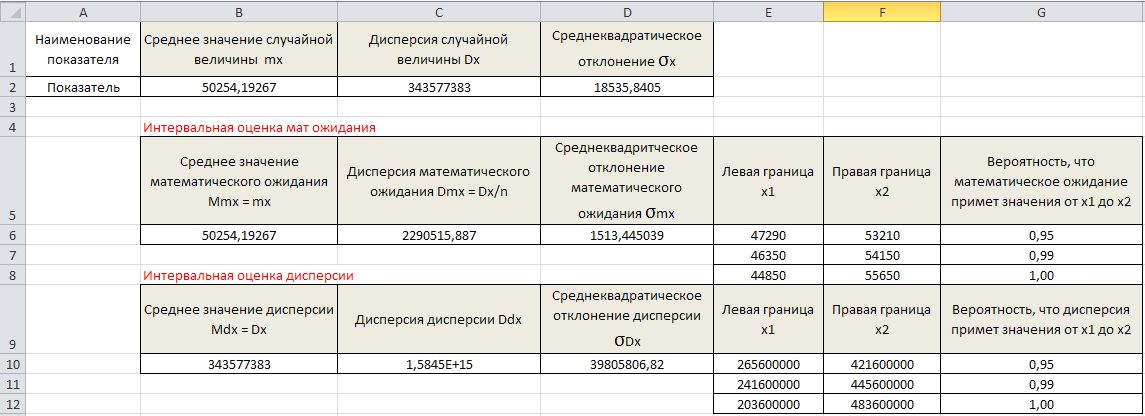
1) добавим таблицу для расчета интервальной оценки математического ожидания с тремя столбцами (рис. 15): «Среднее значение математического ожидания mmx»; «Дисперсия математического ожидания Dmx»; «Среднеквадратическое отклонение σmx» их значения находятся по формулам:
Среднее значение математического ожидания: mmx = mx (т.е. среднее значение математического ожидания совпадает со средним значением случайной величины Х1‑ 50254,19267.
Дисперсия математического ожидания: Dmx = Dx/n = 343577383/150 = 2290515,887 (т.е. значения дисперсии случайной величины Х1 разделить на количество опытов, т.е. 150).
Среднеквадратическое отклонение математического ожидания: 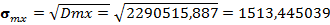 (корень квадратный из дисперсии математического ожидания).
(корень квадратный из дисперсии математического ожидания).
2) разброс значений математического ождиания и дисперсии подчиняется нормальному закону распределения (рис. 16). Используя Mathcad14 найдем интервал (левую и правую границу) для оценки математического ожидания по следующему алгоритму:

| Рис. 16 Нормальный закон распределения |
- в Mathcad введем среднее значение математического ожидания; среднеквадратическое отклонение и функцию f(x) нормального закона распределения, которая задается формулой на рис. 17;
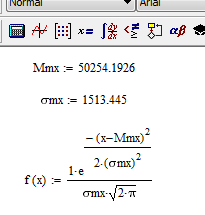
| Рис. 17 Среднее значение, среднеквадратического отклонения математического ожидания и функция нормального закона распределения f(x) |
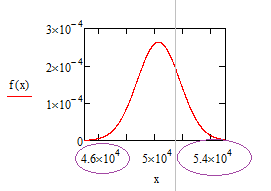
- построим график нормального закона распределения с заданными mmx и σmx
View – Toolbars – Graph и нажать кнопку  . По оси ординат зададим функцию f(x), абсцисс – x и получим график функции изображенной на рис. 17.
. По оси ординат зададим функцию f(x), абсцисс – x и получим график функции изображенной на рис. 17.
Для того чтобы увидеть график необходимо «отрегулировать» границы по оси Х. Известно, что среднее значение математического ожидания равно 50254,1926 является центром симметрии графика. Соответственно, чтобы увидеть график целиком, нужно взять левую границу меньше, а правую больше 50254,1926 на некоторое число q.
Подсказка: Для определения границ целесообразно взять значение q равным
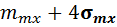
Аналогично необходимо отрегулировать границы по оси ординат. Например, первоначально верхнюю границу функции f(x) задать равной 0,001, нижнюю – 0. Изменяя верхнюю границу f(x), левую и правую границы x добиться изображения графика как на рис. 17.
- на следующем шаге необходимо найти интервал варьирования значений математического ожидания для выбранного значения доверительной вероятности
Введем переменные: x1, x2 – левая и правая границы искомого интервала, которая находится путем добавления или вычитания некоторого числа ε от математического ожидания mmx, т.е. x1 = mmx- ε; x2 = mmx+ ε.
Пусть необходимо определить интервал, в котором будет находиться математическое ожидание с вероятностью 0,95. Для этого необходимо написать формулу определенного интеграла нормального закона распределения в границах от x1 до x2 (рис. 18).
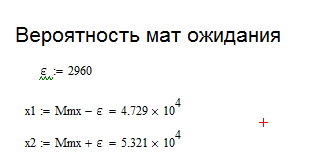
| Рис.18 Расчет доверительного интервала математического ожидания с вероятностью 0,95 |
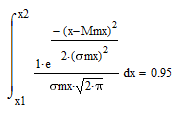
Зададимся ε любым целым числом, например 1200. В результате будут посчитаны значения x1,x2 и определенный интеграл, который позволяет определить значение вероятности попадания математического ожидания в интервал от х1 до х2. Изменяя значение ε можно подобрать вероятность попадания математического ожидания в интервал от х1 до х2. Например, на рис. 18 с вероятностью 0,95 математическое ожидание попадет в интервал от 4,729*104 до 5,321*104.
Аналогично подбираем значение ε для вероятностей попадания математического ожидания равных 0,99 и 1 (рис. 19).
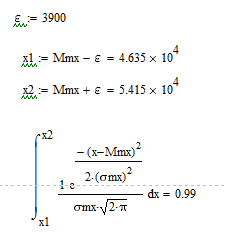
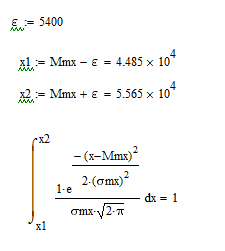
| Рис.19 Расчет доверительного интервала математического ожидания с вероятностью 0,99 и 1 |
 2015-02-04
2015-02-04 2414
2414
