2015-02-04
14649
Задача
1. Определить, какое равенство точнее 9/11 или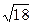 
= 4.24?
Решение. Находим значения данных выражений с большим числом десятичных знаков: a 1 = 9/11 = 0.8181818…, a 2 = 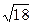= 4.2426…. Затем вычисляем предельные абсолютные погрешности, округляя их с избытком:
Δ a 1 = |0.181818 – 0.818| ≤ 0.00019, Δ a 2 = |4.2426 – 4.24| ≤ 0.0027.
Предельные относительные погрешности составляют
δ a 1 =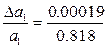 
= 0.00024 = 0.024 %;
δ a 2 =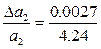 
= 0.00064 = 0.064 %.
Так как δ a 1 < δ a 2, то равенство 9/11 = 0.818 является более точным.
2. Округлить сомнительные цифры числа 72.353(±0.026), оставив верные знаки в узком смысле.
Решение. Пусть 72.353(±0.026) = a. Согласно условию, погрешность Δ a = 0.026 < 0.05; это означает, что в числе 72.353 верными в узком смысле являются цифры 7, 2, 3. По правилам округления найдём приближённое значение числа, сохранив десятые доли:
a 1 = 72.4; Δ a 1 = Δ a + Δ OKP = 0.026 + 0.047 = 0.073.
Полученная погрешность больше 0.05; значит, нужно уменьшить число цифр в приближённом числе до двух:
a 2 = 72; Δ a 2 = Δ a + Δ OKP = 0.026 + 0.353 = 0.379.
Так как Δ a 2 < 0.5, то обе оставшиеся цифры верны в узком смысле.
Округлить сомнительные цифры числа 2.3544; δ = 0.2 %, оставив верные знаки в широком смысле.
Решение. Пусть a = 2.3544; δ a = 0.2 %; тогда Δ a = a ·δ a = 0.00471. В данном числе верными в широком смысле являются три цифры, поэтому округляем его, сохраняя эти три цифры:
a 1 = 2.35; Δ a 1 = 0.0044 + 0.00471 = 0.00911 < 0.01.
Значит, в округлённом числе 2.35 все три цифры верны в широком смысле.
3. Найти предельные абсолютные и относительные погрешности числа 0.4357, если они имеют только верные цифры в узком смысле.
Решение. Так как все четыре цифры числа a = 0.4357 верны в узком смысле, то абсолютная погрешность Δ a = 0.00005, а относительная погрешность
Δ a = 1/(2·4·103) = 0.000125 = 0.0125 %
Найти предельные абсолютные и относительные погрешности числа 12.384, если они имеют только верные цифры в широком смысле.
Решение. Так как все пять цифр числа a = 12.384 верны в широком смысле, то Δ a = 0.001, δa = 1/104 = 0.0001 = 0.01 %
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2. Изучение численных методов решения уравнений (3 ч)
Цель работы – дать студенту возможность изучить алгоритмы и методы нахождения корней нелинейных уравнений.
Теоретические сведения.
Задача нахождения корней линейных уравнений вида встречается в различных областях научных исследований (здесь – некоторая непрерывная функция). Нелинейные уравнения можно разделить на два класса – алгебраические и трансцендентные. Алгебраическими уравнениями называются уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). В частности, многочлен является целой алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и др.), называются трансцендентными.
Методы решения нелинейных уравнений делятся на прямые и итерационные. Прямые методы позволяют записать корни в виде некоторого конечного соотношения (формулы).
Однако встречающиеся на практике уравнения не удаётся решить такими простыми методами. Для их решения используются итерационные методы, т. е. методы последовательных приближений.
Метод половинного деления
В методе половинного деления (дихотомии, бисекции) заданный отрезок [a, b] разделим пополам (рисунок 2) и положим x 0 = (a + b)/2.Из двух полученных отрезков [a; х 0] и [ x 0; b] выбираем тот, на концах которого функция f (x) имеет противоположные знаки. Полученный отрезок снова делим пополам и приводим те же рассуждения. Процесс продолжаем до тех пор, пока длина отрезка, на концах которого функция имеет противоположные знаки, не будет меньше заданного ε, любую точку отрезка с точностью ε можно принять за корень уравнения f (x) = 0.
Таким образом, если x 0 и x 1 таковы, что f (x 0)· f (x 1) < 0, то полагаем x 2 = (x 0 + x 1)/2 и вычисляем f (x 2). Если f (x 2) = 0, то корень найден. В противном случае из отрезков [ х 0; х 2] и [ х 2; х 1] выбирам тот, на концах которого f принимает значения разных знаков, и проделываем аналогичную операцию. Процесс продолжаем до получения требуемой точности.
 |
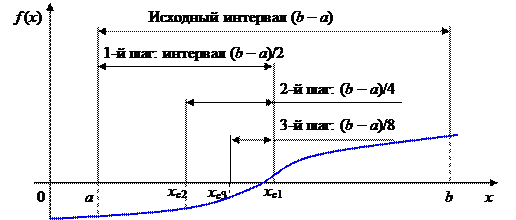Рисунок 2 – Метод половинного деления (дихотомии)
Пример 1. Составить программу для нахождения корней методом половинного деления для функции f (x) = x 2 + 1.7 x + 1.7 по схеме алгоритма.
