Решение. Первоначально корни уравнения определяем с точностью ε = 0.1 графическим методом, а затем найденное значение корня уточняем до 0.0001

Первоначально корни уравнения определяем с точностью ε = 0.1 графическим методом, а затем найденное значение корня уточняем до 0.0001.

Перепишем уравнение в виде

.

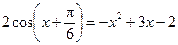Если построить два графика: 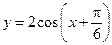и 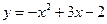, то можно убедиться, что один корень равен ≈1.1, а второй – ≈2.9. Поэтому первый интервал выбираем [0.9; 1.3], второй – [2.7; 3.1].

Метод линейной интерполяции

Если x ₀, x ₁ – приближённые значения корня уравнения f (x) = 0, a f (x ₁) · f (x ₂) < 0, то последующие приближения находят по формуле

.

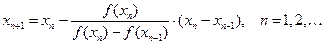Методом хорд называют также метод, при котором один и концов отрезка [a; b] закреплён (рис. 8), т. е. вычисление приближения корня уравнения f (x) = 0 производят по формулам

.

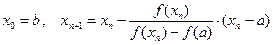
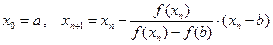При расчёте предполагается, что корень уравнения находится на отрезке [а; b], a f "(x) сохраняет знак на [а; b].

Из рисунка 8 видно, что получаемые точки x_c постепенно сходятся к корню уравнения. Поскольку в рассмотренном методе очередное приближение x_c определяется с помощью интерполяции, учитывающей наклон кривой f (x), он во многих случаях ока­зывается более эффективным, чем метод половинного деления.

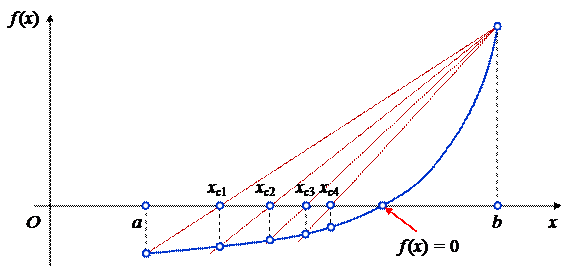Рисунок 8 – Метод хорд

Пример 5. Методом хорд найти корень уравнения 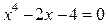с точностью до 0.01.

Решение

Положительный корень будет находиться на отрезке [1; 1.7], так как

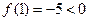, а .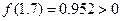

Найдём первое приближённое значение корня по формуле

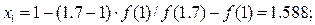
Так как f (1.588) = –0.817 < 0, то применяя вторично способ хорд к отрезку [1.588; 1.7], найдём второе приближённое значение корня:

.

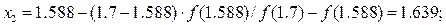
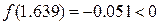Теперь найдём третье приближённое значение:

;

.

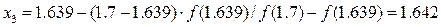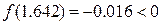После этого найдём четвёртое приближённое значение:

;

.

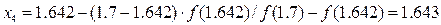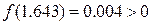Следовательно, искомый корень с точностью до 0.01 равен 1.64.

Комбинированный метод секущих – хорд

Этот метод обеспечивает гарантированную сходимость при выборе в пределах отрезка [ a, b ] двух приближений: нулевого x ₀ и первого x ₁. Он реализуется алгоритмом, описываемым для метода Ньютона с заменой производной F ′(x) её приближённым значением – множитель перед F (x_n):

.

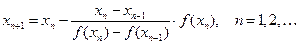На рисунке 9 показана схема алгоритма комбинированного метода секщих – хорд.

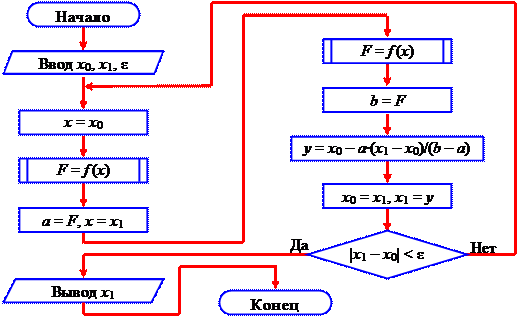Рисунок 9 – Схема алгоритма метода секущих – хорд

Метод Ньютона

Если х ₀ – начальное приближение корня уравнения f (x) = 0, то последовательные приближения находят по формуле

.

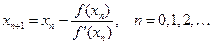Если f ′ и f ″ (первая и вторая производные) непрерывны и сохраняют определённые знаки на отрезке [ a; b], а f (a) · f (b) < 0, то, исходя из начального приближения 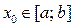, удовлетворяющего условию f (x₀)·f "(x₀) < 0, можно вычислить с любой точностью единственный корень уравнения f (x) = 0.

На практике часто используют модификации метода Ньютона, свободные от этого недостатка. Одно из упрощений сводится к тому, что производная вычисляется только один раз в начальной точке и затем это значение используется на всех последующих шагах. Данная модификация основывается на предположении о малом изменении производной вблизи корня.

Одной из наиболее известных модификаций является метод секущих. В этом методе производная заменяется её приближённым значением:

.

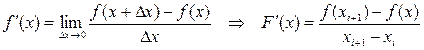В формуле для F'(x) в отличие от f ′(x) приращение 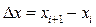, полагается малым, но Δ x ≠ 0. Геометрически это означает, что приближённым значением корня считается точка пересечения секущей, проходящей через две точки функции f (x_i) и f (x_i + h), с осью абсцисс. Схема метода Ньютона показана на рисунке 10 a.

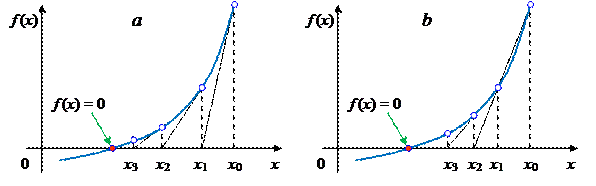Рисунок 10 – Метод Ньютона (a) и метод секущих (b)

Выберем на отрезке [ a; b] произвольную точку x ₀ – нулевое приближение. Затем найдём

,

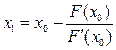далее

.

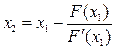Таким образом, процесс нахождения корня уравнения сводится к вычислению чисел x_n по формуле

.

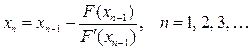Процесс вычисления продолжается до тех пор, пока не будет выполнено условие

.

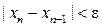Схема итерационного процесса метода Ньютона приведена на рисунке 11, из которого понятно, что каждое следующее приближение может быть определено по формуле

.

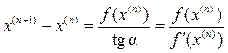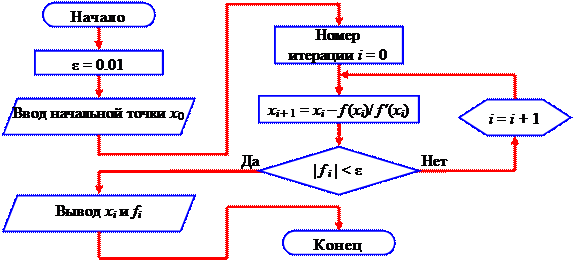Рисунок 11 – Схема алгоритма метода Ньютона

Пример 6. Методом Ньютона (касательных) найти корень уравнения 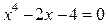с точностью до 0.01.

Решение

В этом уравнении

f (x) = 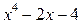, f '(x) = 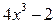, а f "(x) = 12 x ².

Так как f (x) и f "(x) при x₀ = 1.7 имеют один и тот же знак, а именно f (1.7) = 0.952 > 0 и f "(1.7) > 0, то применяем формулу

,

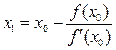где f ′(1.7) = 4 1.7³ – 2 = 17.652.

Тогда

.

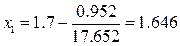Применяем второй раз способ касательных:

,

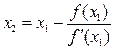где f (x ₁) = f (1.646) = 0.048, f ′(1.646) = 15.838;

;

; ;

.

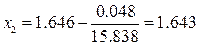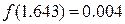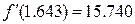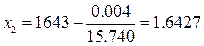Следовательно, искомый корень с точностью до 0.01 равен 1.64.

Пример 7. Методом Ньютона (касательных) найти действительный корень уравнения .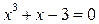

Решение

Записав данное уравнение в виде x ³ = –х + 3 и построив графики функций f ₁ (x) = x ³ и f ₂ (x) = – х + 3, найдем, что единственный корень уравнения принадлежит отрезку [1; 2].

Определим отрезок меньшей длины, на котором находится корень.

Так как 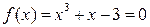, f (1.2) = (1.2)³ + 1.2 – 3 = –0.072 < 0,

f (1.3) = (1.3)³ + 1.3 – 3 = 0.497 > 0, то корень лежит на отрезке [1.2; 1.3]. Серединой этого отрезка является точка x = 1.25. Поскольку f (1.25) = (1.25)³ + 1.25 – 3 = 0.203125 > 0 и f (1.2) < 0, то искомый корень принадлежит отрезку [1.20; 1.25]. Данная функция 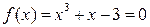имеет производные f '(x) = 3 х ² + 1, f "(x) = 6 x, принимающие положительные значения на отрезке [1.20; 1.25]. В качестве начального приближения выберем x = 1.25.

Результаты вычислений записываем в таблице 1, из которой видно, что искомый корень x = 1.21341.

Таблица 1 – Метод касательных

n	xn	f (xn) = xn 3 + xn – 3	f ′(xn) = x 3 n +1	xn +1
	1.25	0.203125	5.6875	1.214286
	1.214286	0.004738	5.42347	1.213412
	1.213412	0.000002	5.417107	1.213412