Системы и совокупности уравнений с одной переменной

Пусть даны уравнения 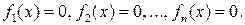Если требуется найти все значения 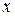, которые удовлетворяют всем заданным уравнениям одновременно, то говорят, что дана система 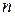уравнений. Для обозначения системы используют фигурную скобку:

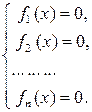
Другими словами в системе 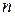уравнений – есть конъюнкция уравнений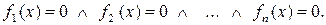

Пример. Рассмотрим уравнение 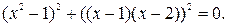Ясно, что 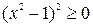и 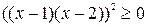, а сумма двух неотрицательных чисел равна нулю и только тогда, когда каждое слагаемое равно нулю. Поэтому сначала решают уравнения 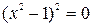и 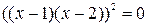, а затем находят их общие корни. Корнями уравнения 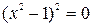служат числа 1 и –1, а корнями уравнения 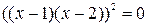– числа 1 и 2. Общим является число 1 – это корень исходного уравнения.

Если требуется найти все значения 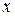, которые удовлетворяют хотя бы одному из данных уравнений, то говорят, что дана совокупность 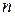уравнений.

Для обозначения совокупности используют квадратную скобку:

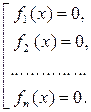
Другими словами система 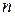уравнений – есть дизъюнкция уравнений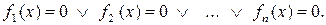

Пример. Рассмотрим уравнение: 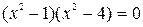. Произведение двух чисел равно нулю тогда и только тогда, когда хотя бы одно из чисел равно нулю. Поэтому сначала решают уравнения 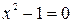и 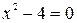, а затем объединяют их корни. Корнями первого уравнения являются числа 1 и –1, а корнями второго – числа 2 и –2. Значит, 1; –1; 2; –2 – корни исходного уравнения.