Имеем: f (x) = x 3,
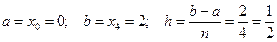 ,
,
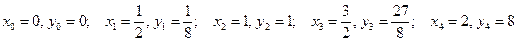 ;
;
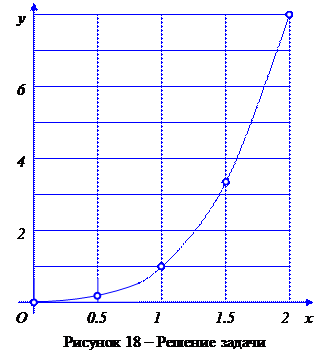 (рисунок 18)
(рисунок 18)
a) по формуле прямоугольников:
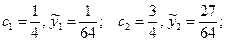
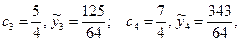
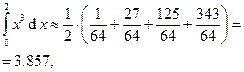
т. е. 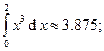
b) по формуле трапеций:
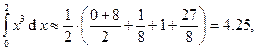
т. е. 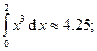
c) по формуле парабол:
 т. е.
т. е. 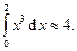
Точное значение интеграла 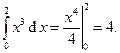
Абсолютные погрешности соответствующих формул таковы: a) 0.125; b) 0.25; c) 0.
Задача
Вычислить интегралы с помощью формулы Симпсона, разбив отрезок интегрирования на 10 равных частей. Все вычисления проводить с округлением до третьего десятчного знака.
Варианты
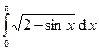
| 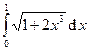
| ||
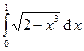
| 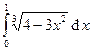
| ||
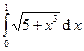
| 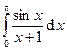
| ||
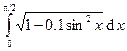
| 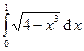
| ||
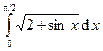
| 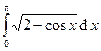
| ||
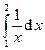
| 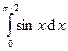
| ||
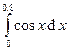
| 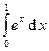
| ||
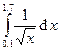
| 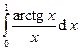
| ||
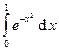
| 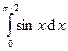
|
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 5. Ознакомление с численными методами решения обыкновенных дифференциальных уравнений (3 ч)
Цель работы – дать студенту возможность изучить алгоритмы и методы решения обыкновенных дифференциальных уравнений.
Теоретические сведения.
Обыкновенными дифференциальными уравнениями описать задачи движения системы взаимодействующих материальных точек, химической кинетики, электрических цепей, сопротивления материалов, спроса и предложения и многие другие.
Дифференциальным уравнением называется уравнение, связывающее аргумент, функцию этого аргумента и производные этой функции до некоторого порядка включительно. Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком уравнения.
Различают обыкновенные дифференциальные уравнения (ОДУ) и дифференциальные уравнения в частных производных (ДУЧП).
Решением дифференциального уравнения называют любую функцию, при подстановке которой в это уравнение получается тождество. График решения дифференциального уравнения называется интегральной кривой этого уравнения.
  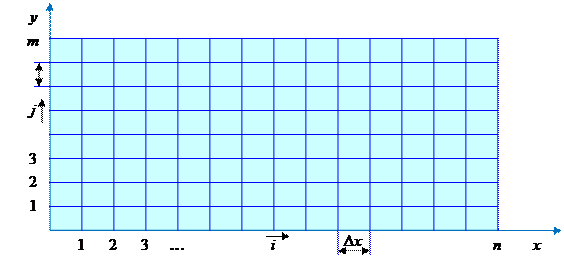 |
Рисунок 19 – Ортогональная сетка
Построение численных алгоритмов решения уравнения (22.1) опирается на дискретизацию задачи.
Введём в области расчёта 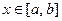 дискретный набор точек
дискретный набор точек 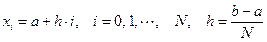 , в которых будет вычисляться приближённое решение.
, в которых будет вычисляться приближённое решение.
Точки xi будем называть узлами интегрирования или узлами сетки (рисунок 19), расстояние h между узлами – шагом интегрирования или шагом сетки. Совокупность всех узлов 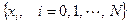 будем называть сеточной областью или просто сеткой узлов.
будем называть сеточной областью или просто сеткой узлов.
Также будем пользоваться другими обозначениями:
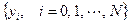 – совокупность искомых приближённых значений решения задачи в узлах сетки;
– совокупность искомых приближённых значений решения задачи в узлах сетки;
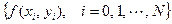 – совокупность значений правой части уравнения в узлах.
– совокупность значений правой части уравнения в узлах.
Различные совокупности величин, отнесённых к узлам сетки, называются сеточными функциями.
Для характеристики точности численных методов определим погрешность приближённого решения следующим образом:
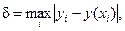
где y (xi) – значение точного решения в узле сетки.
Метод, по которому получено численное решение, является методом p -го порядка точности, если выполняется неравенство
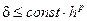 .
.
Переходим к обсуждению конкретных методов получения приближённого решения задачи в узлах сетки.
Простейший способ их конструирования опирается на замену производной в левой части уравнения в окрестности каждого узла приближённым разностным отношением по формулам численного дифференцирования.
Метод Эйлера.
Заменяя в (22.1) производную в окрестности каждого i -го узла сетки разностным отношением, приходим к методу Эйлера:
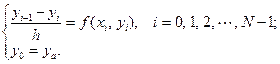 (23.1)
(23.1)
Алгебраические соотношения между компонентами сеточной функции, которыми заменяются исходные дифференциальные уравнения в окресности каждого узла сетки, будем называть разностными уравнениями (соотношениями).
Замкнутую систему разностных уравнений вместе с дополнительными условиями (начальными или краевыми) называют разностной схемой. Таким образом, (23.1) – это разностная схема Эйлера.
Последовательные значения yi вычисляются по формуле
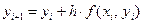 , (23.2)
, (23.2)
которая непосредственно следует из соотношения (23.1).
Метод Эйлера имеет очень простую геометрическую интерпретацию. Искомая интегральная кривая y (x) на отрезке [ a, b ] приближается к ломаной (рисунок 20), наклон которой на каждом элементарном участке [ xi, xi +1] определяется наклоном интегральной кривой уравнения в точке (xi, yi).
К этому же методу можно придти, заменяя производную в уравнении (23.2) разностным отношением
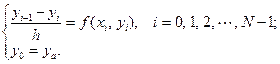
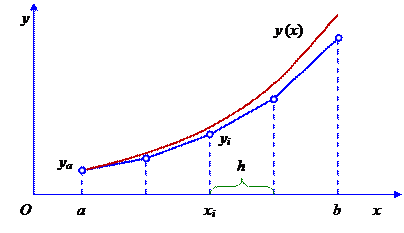 |
Рисунок 20 – Интегральная кривая
Последовательные значения yi в этом случае вычисляются по формуле
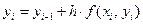 .
.
Однако при этом возникают некоторые трудности, связанные с тем, что искомая величина yi входит в правую часть уравнения, причём, в общем случае, нелинейным образом. Эти трудности не принципиальны, достаточно вспомнить о методах решения нелинейных уравнений.
Например, можно предложить следующий итерационный процесс для вычисления приближённого решения в очередном i -м узле
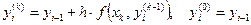 .
.
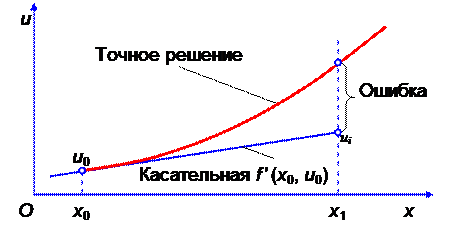 |
Рисунок 21 – Начальный шаг метода Эйлера
Такого рода методы, в которых для вычисления приближённого решения в очередном i -м узле необходимо дополнительно решать некоторые уравнения (линейные или нелинейные), называются неявными методами. В противоположность этому методы, в которых приближённое решение в очередном i -м узле явно выражается через предыдущие значения yi –1, yi –2, …, называются явными методами. При этом, если для вычисления yi используется только одно предыдущее значение yi –1, то метод называется одношаговым, а если несколько предыдущих значений – многошаговым. Таким образом, метод Эйлера является явным одношаговым методом (рисунок 21).
В основе метода Эйлера лежит идея графического построения решения дифференциального уравнения. Однако этот метод даёт одновременно и способ нахождения искомой функции в табличной форме.
Пусть дано дифференциальное уравнение y ' = f (x, y). Найти приближённое численное решение этого дифференциального уравнения, т. е. составить таблицу приближённых значений функции y = y (x), удовлетворяющей заданным начальным условиям
| x | x 1 | x 2 | x 3 | x 4 | x 5 | x 6 | … | xn |
| y | y 1 | y 2 | y 3 | y 4 | y 5 | y 6 | … | yn |
где 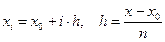 – шаг таблицы.
– шаг таблицы.
Приближённо можно считать, что правая часть в y ' = f (x, y) остаётся постоянной на каждом из отрезков между точками деления. Метод Эйлера состоит в непосредственной замене производной разностными отношениями по приближённой формуле
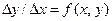 ;
; 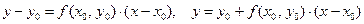 ;
;
если x = x 1, то
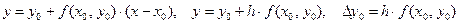 ;
;
если x = x 2, то
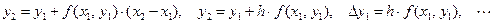
если x = xi +1, то 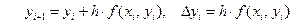 .
.
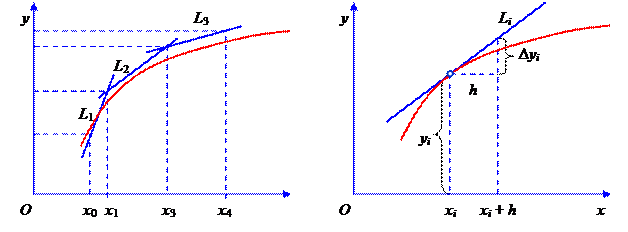 |
Рисунок 22 – Интегральная кривая Рисунок 23 – Касательная к кривой
Таким образом, получение таблицы значений искомой функции y (x) по методу Эйлера заключается в циклическом применении пары формул
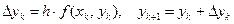 ,
,
где k = 0, 1, 2, …, n.
Геометрически эти формулы означают, что на отрезке [ xi; xi +1] интегральная кривая заменяется отрезком касательной к кривой (рисунки 22, 23).
Пример 21. Проинтегрировать методом Эйлера дифференциальное уравнение 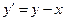 с начальными условиями x 0 = 0; y 0 = 1.5 на отрезке [0; 1.5] при h = 0.25.
с начальными условиями x 0 = 0; y 0 = 1.5 на отрезке [0; 1.5] при h = 0.25.
 2015-02-04
2015-02-04 524
524








