Перепишем заданное дифференциальное уравнение в виде:
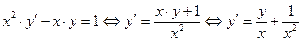 .
.
Здесь  . Найдём числа:
. Найдём числа:
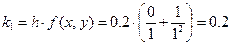 ;
;
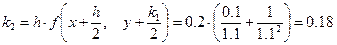 ;
;
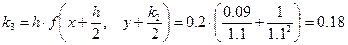 ;
;
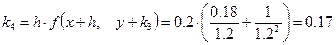 .
.
Следовательно,
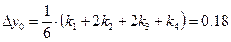 , т. е.
, т. е. 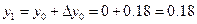 .
.
Аналогичным образом находим
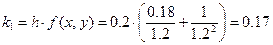 ;
;
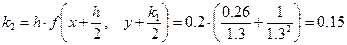 ;
;
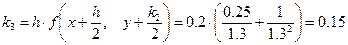 ;
;
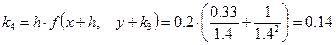 .
.
Следовательно,
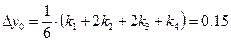 , т. е.
, т. е. 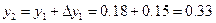 и т. д.
и т. д.
Используя метод Эйлера, составить таблицу приближённых значений интеграла дифференциального уравнениния y' = f (x, y), удовлетворяющего начальным условиям y (x 0) = y 0 на отрезке [ a, b ]; шаг h = 0.1. Все вычисления вести с четырьмя десятичными знаками.
Варианты
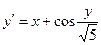 , ,
| y 0(1.8) = 2.6 | x 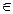 [1.8; 2.8] [1.8; 2.8]
| |
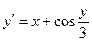 , ,
| y 0(1.6) = 4.6 | x  [1.6; 2.6] [1.6; 2.6]
| |
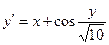 , ,
| y 0(0.6) = 0.8 | x  [0.6; 1.6] [0.6; 1.6]
| |
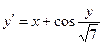 , ,
| y 0(0.5) = 0.6 | x  [0.5; 1.5] [0.5; 1.5]
| |
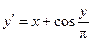 , ,
| y 0(1.7) = 5.3 | x  [1.7; 2.7] [1.7; 2.7]
| |
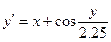 , ,
| y 0(1.4) = 2.5 | x  [1.4; 2.4] [1.4; 2.4]
| |
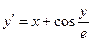 , ,
| y 0(1.4) = 2.5 | x  [1.4; 2.4] [1.4; 2.4]
| |
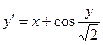 , ,
| y 0(0.8) = 1.4 | x  [0.8; 1.8] [0.8; 1.8]
| |
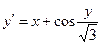 , ,
| y 0(1.2) = 2.1 | x  [1.2; 2.2] [1.2; 2.2]
| |
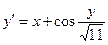 , ,
| y 0(2.1) = 2.5 | x  [2.1; 3.1] [2.1; 3.1]
| |
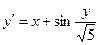 , ,
| y 0(1.8) = 2.6 | x  [1.8; 2.8] [1.8; 2.8]
| |
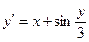 , ,
| y 0(1.6) = 4.6 | x  [1.6; 2.6] [1.6; 2.6]
| |
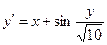 , ,
| y 0(0.6) = 0.8 | x  [0.6; 1.6] [0.6; 1.6]
| |
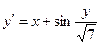 , ,
| y 0(0.5) = 0.6 | x  [0.5; 1.5] [0.5; 1.5]
| |
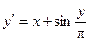 , ,
| y 0(1.7) = 5.3 | x  [1.7; 2.7] [1.7; 2.7]
| |
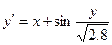 , ,
| y 0(1.4) = 2.2 | x 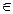 [1.4; 2.4] [1.4; 2.4]
| |
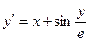 , ,
| y 0(1.4) = 2.5 | x 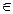 [1.4; 2.4] [1.4; 2.4]
| |
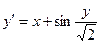 , ,
| y 0(0.8) = 1.3 | x  [0.8; 1.8] [0.8; 1.8]
| |
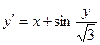 , ,
| y 0(1.1) = 1.5 | x  [1.1; 2.1] [1.1; 2.1]
| |
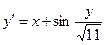 , ,
| y 0(0.6) = 1.2 | x 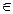 [0.6; 1.6] [0.6; 1.6]
|
 2015-02-04
2015-02-04 345
345







