Решение. Зная пределы интегрирования, a = 1 и b = 9, находим шаг

Зная пределы интегрирования, a = 1 и b = 9, находим шаг

.

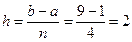Тогда точками разбиения будут

.

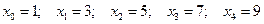Значения подынтегральной функции 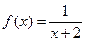в этих точках таковы

.

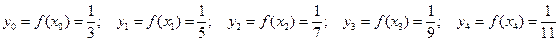Найдём численное значение интеграла по формуле левых прямоугольников:

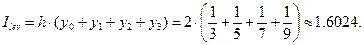
По формуле правых прямоугольников:

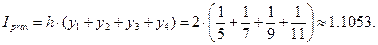
Пример 14. По методу левых прямоугольников вычислить определённый интеграл

.

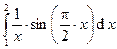Пример 15. По методу правых прямоугольников вычислить определённый интеграл

.

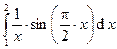Пример 16. По методу средних прямоугольников вычислить определённый интеграл

.

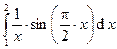Для решения задач по схеме алгоритма составить программу.

Метод трапеций. Формула трапеций имеет следующий вид

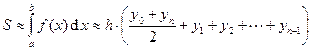. (16.1)

Эта формула означает, что площадь криволинейной трапеции заменяется площадью многоугольника, составленного из n трапеций (рисунок 16.1), при этом кривая заменяется вписанной в неё ломаной. Формулу трапеций получают аналогично формуле прямоугольников: на каждом частичном отрезке криволинейная трапеция заменяется обычной.

Разобьём отрезок [ a, b ] на n равных частей длины 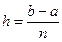. Абсциссы точек деления a = x ₀, x ₁, x ₂, …, b = x_n (рисунок 15). Пусть y ₀, y ₁, …, y_n – соответствующие им ординаты графика функции. Тогда расчётные формулы для этих значений примут вид .

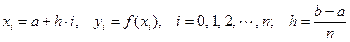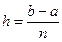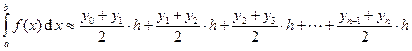Заменим кривую y = f (x) ломаной линией, звенья которой соединяют концы ординат y_i и y_{i +1} (i = 0, 1, 2, …, n). Тогда площадь криволинейной трапеции приближённо равна сумме площадей обычных трапеций с основаниями y_i и y_{i +1} высотой :

или

.

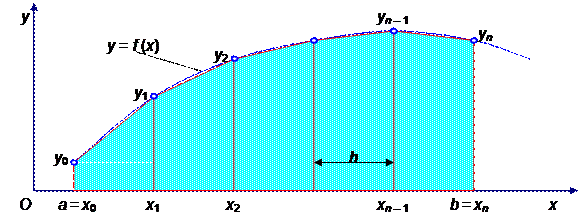Рисунок 15 – К приближённому вычислению интеграла методом трапеций

Пример 17. Пользуясь формулой трапеций вычислить определённый интеграл

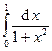при n = 4.