2015-02-04
819
После построения интерполяционного многочлена возникает вопрос, насколько близко построенный многочлен приближается к функции f(x) в точках, отличных от узлов. В этом случае рассматривают остаточный член
| R n(x)|=| f (x) – L n(x)|.
В данном случае Ln(x) – многочлен Лагранжа.
Анализ показывает, что абсолютная погрешность интерполяционной формулы Лагранжа имеет вид
| R n(x)|=| f (x) – L n(x) ≤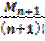 
| П n+1(x)| (3.17)
где M n+1 = max | f (n+1)(x)|, f (n+1)(x) – (n +1)- я производная f (x), а
x≤ a≤b
П n+1(x) = (x – x 0) (x – x 1)… (x – x n).
Пример. С какойточностью можно вычислить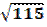 
с помощью интерполяционной формулы Лагранжа второй степени функции у = 
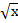, выбрав узлы интерполяции х0 = 100,х1 = 121, х2 = 144
Решение. Вычислим первую, вторую и третью производные функции: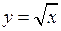 
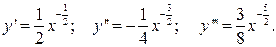
Отсюда очевидно, что максимальное значение М3 будет, если из отрезка [100,144] выбрать x = 100, т.е.
M 3 = max | y ’’’ | =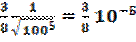 
при 100 ≤ х ≤ 144.
На основании формулы (3.17) получаем
| R 2| ≤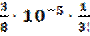 
|(115-100)(115-121)(115-144) | 
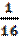· 10-5·15·6·29 ≈ 1,6 · 10-3.
Для первой интерполяционной формулы Ньютона (3.11) остаточный член Rn(х) представляется в виде
Rn(х) = h(n+1)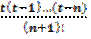 
f(n+1)(ξ) (3.18)
где ξ – некоторое промежуточное значение между узлами интерполирования х 0, х 1, х 2,…, х n и рассматриваемой точкой х; h = x i+1 – x i; t =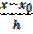 
.
Аналогично получается остаточный член для второй интерполяционной формулы Ньютона (3.13), только здесь t =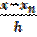 
:
R (x) = h n+1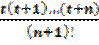 
f (n +1 )(ξ).
Пример. Оценить погрешность приближения функции f (x) = sin x интерполяционным полиномом пятой степени F 5 (x),совпадающим с данной функцией при значениях x = 00, 50, 100, 150, 200, 250.
Решение. Здесь f (6) (x) = - sin x,поэтому | f (6) (x) | ≤ 1.На основании формулы (3.18) имеем
|sin x – F 5(x)| ≤ h n+1 |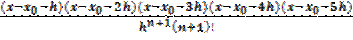 
| <
< 
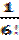| x 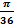(x - 
)(x -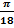 
) (x - 
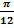) (x - 
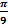) (x - 
) |.
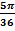Если, например, х = 12030’ = arc 0,21816,получим
|sin x – F 5(x)| < 2,2 · 10-9.
