Пусть расположение опытных точек таково, что они лежат вблизи прямой L (см. рис.2). В этом случае эмпирическую формулу будем искать в виде линейной функции
| y=ax+b. | (4.2) |
Для нахождения параметров a и b применяют несколько способов.
1) Способ натянутой нити. Строим точечный график на миллиметровой бумаге в достаточно крупном масштабе. Проводим прямую, близкую к опытным данным. Измеряем отрезок, отсекаемый прямой на оси ординат, это будет b. Найдем tg угла между прямой и осью абсцисс, это будет a. Эмпирическая формула готова. (b =0,147 при x =10; y =1,138; 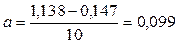 ).
).
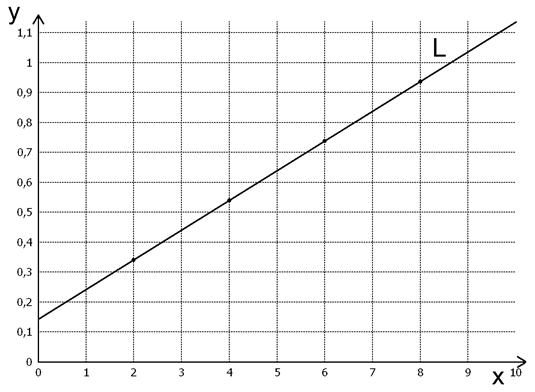
Рис.2
2) Способ выбранных точек. Для нахождения параметров a и b измеряют координаты двух точек 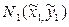 и
и 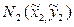 , лежащих на прямой L и по возможности удаленных друг от друга. Тогда a и b могут быть определены из системы уравнений
, лежащих на прямой L и по возможности удаленных друг от друга. Тогда a и b могут быть определены из системы уравнений
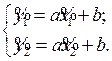
3) Способ средней. Пусть опытные значения записаны в таблице.
| x | 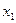 | 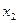 | 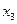 | … | 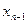 | 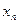 |
| y | 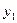 | 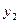 | 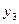 | … | 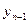 | 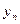 |
Равенство (4.1) запишем в виде
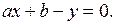 (4.3)
(4.3)
Если вместо x и y представить какие-нибудь опытные значения, то, так как они приближенные, получим не нуль, а некоторое малое число 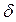 , называемое невязкой. Например,
, называемое невязкой. Например, 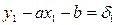 ,
, 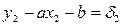 , и т. д. Все ошибки носят случайный характер. Поэтому при довольно большом числе измерений положительные и отрицательные невязки уравниваются, и сумма всех невязок равна нулю.
, и т. д. Все ошибки носят случайный характер. Поэтому при довольно большом числе измерений положительные и отрицательные невязки уравниваются, и сумма всех невязок равна нулю.
Отсюда укажем способ отыскания чисел a и b в уравнении (4.2). Все опытные точки разделим на две группы, одинаковые или почти одинаковые по числу точек (В общем случае все опытные точки разбиваются на столько групп, сколько неизвестных в эмпирической формуле. Так, для параболы разбиваем на три группы). Для всех уравнений первой группы найдем невязки и суммы их приравняем нулю. То же проделаем для уравнений второй группы. При этом числа a и b остаются неизвестными. Мы получили два линейных уравнения с двумя неизвестными. Решая систему, найдем a и b.
Пример. Зависимость y от x дается таблицей.
| x | ||||||||||
| y | 1,02 | 2,50 | 3,92 | 5,16 | 6,82 | 8,36 | 10,74 | 11,82 | 13,64 | 12,96 |
По этим данным построим эмпирическую формулу разными способами.
Сначала строим на миллиметровой бумаге точечный график и проводим приближающую прямую. Видно, что это прямая линия (рис.3).
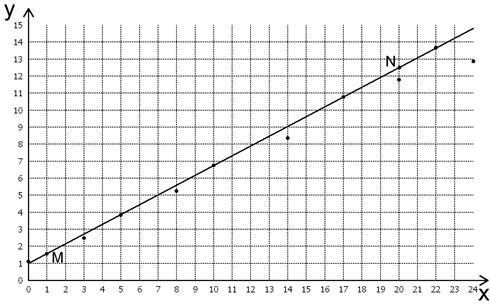
Рис.3
Решение способом натянутой нити.
Из рис.3 видно, что прямая отсекает на оси ординат отрезок, равный 0,98. Далее измеряем tg угла наклона между прямой и осью абсцисс. Он равен 0,55. Эмпирическая формула будет y = 0,55 x + 0,98.
Решение способом выбранных точек.
На прямой берем произвольные точки M и N и находим их координаты: M(1,0; 1,5), N(20,0; 12,3). Подставляем их в равенство y = ax + b, получаем систему уравнений:
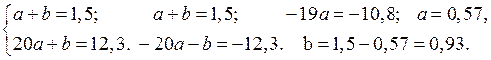
Решая, находим y = 0,57 x + 0,93.
Решение способом средней.
Разделим все опытные точки на две группы. В первую группу войдут первые пять точек, во вторую – остальные. Пользуясь записью (4.3) найдем невязки для точек первой группы и сумму невязок приравняем нулю
(b –1,02)+(3 a + b– 2,50)+(5 a + b –3,92)+(8 a + b –5,16)+(10 a + b –6,82) = 0
То же сделаем для точек второй группы.
(14 a + b –8,36)+(17 a + b– 10,74)+(20 a + b –11,82)+(22 a + b –13,64)+(24 a + b –12,96) = 0
Опуская скобки и приводя подобные члены, получаем:
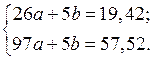
Решая эту систему, получаем:
a = 0,565; b = 0,940;
y = 0,565 x + 0,940.
 2015-02-04
2015-02-04 2129
2129








